题目内容
【题目】如图,△ABC是等边三角形,点E,F分别在BC,AC上,且BE=CF,连结AE与BF相交于点G.将△ABC沿AB边折叠得到△ABD,连结DG.延长EA到点H,使得AH=BG,连结DH.
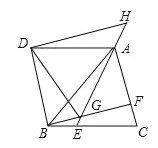
(1)求证:四边形DBCA是菱形.
(2)若菱形DBCA的面积为8![]() ,
,![]() ,求△DGH的面积.
,求△DGH的面积.
【答案】(1)四边形DBCA是菱形(证明过程见解析)(2)S△DGH=![]() .
.
【解析】
试题分析:(1)利用等边三角形的性质和折叠的定义,可知AC=AD=BC=BD,利用菱形的判定定理可得结论;
(2)首先证得△ABE≌△BCF(SAS),再由菱形的性质和全等三角形的判定证得△DBG≌△DAH(SAS),由全等三角形的性质和相似三角形的判定可证得△DBA∽△DGH,由相似三角形的性质面积比等于相似比的平方,可得结果.
试题解析:证明:∵△ABC是等边三角形,
∴AC=BC由折叠知AC=AD,BC=BD,
∴AC=AD=BC=BD,
∴四边形DBCA是菱形;
(2)解:∵△ABC是等边三角形,
∴AB=BC,∠ABC=∠C=60°,
在△ABE与△BCF中,
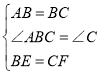 ,
,
∴△ABE≌△BCF(SAS),
∴∠AEB=∠BFC,
∵四边形DBCA是菱形,
∴DA∥BC,DB∥AC,∠BDA=∠C=60°,
∴∠HAD=∠AEB,∠DBG=∠BFC,
∴∠HAD=∠DBG,
在△DBG与△DAH中,
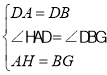 ,
,
∴△DBG≌△DAH(SAS),
∴DG=DH,∠BDG=∠ADH,
∴∠HDG=∠ADH+∠GDA=∠BDG+∠GDA=∠BDA=60°,
又∵DA=DB,DG=DH,
∴△DBA∽△DGH,
∴![]() ,
,
∵S△DBA=![]() S菱形DBCA=
S菱形DBCA=![]() ,
,
∴S△DGH=![]() .
.

练习册系列答案
 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目