Question

【题目】如图，在△ABC中，D、E分别是AB、AC的中点，BE=2DE，过点C作CF∥BE交DE的延长线于F．

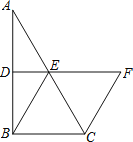
（1）求证：四边形BCFE是菱形；

（2）若CE=4，∠BCF=120°，求菱形BCFE的面积．

Answer 1

【答案】（1）见解析（1）

【解析】

试题分析：（1）由题意易得，EF与BC平行且相等，故四边形BCFE是平行四边形．又邻边EF=BE，则四边形BCFE是菱形；

（2）连结BF，交CE于点O．利用菱形的性质和等边三角形的判定推知△BCE是等边三角形．通过解直角△BOC求得BO的长度，则BF=2BO．利用菱形的面积=CEBF进行解答．

（1）证明：∵D、E分别是AB、AC的中点，

∴DE∥BC，BC=2DE．

∵CF∥BE，

∴四边形BCFE是平行四边形．

∵BE=2DE，BC=2DE，

∴BE=BC．

∴□BCFE是菱形；

（2）解：连结BF，交CE于点O．

∵四边形BCFE是菱形，∠BCF=120°，

∴∠BCE=∠FCE=60°，BF⊥CE，

∴△BCE是等边三角形．

∴BC=CE=4．

∴．

∴．