题目内容
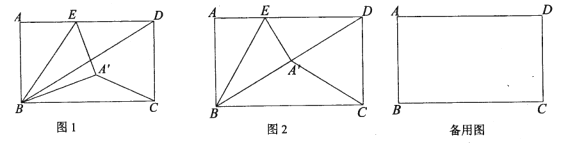
【题目】如图,在矩形![]() 中,
中,![]() ,点E是
,点E是![]() 边上的动点,将矩形
边上的动点,将矩形![]() 沿
沿![]() 折叠,点A落在点
折叠,点A落在点![]() 处,连接
处,连接![]() .
.
(1)如图,求证:![]() ;
;
(2)如图,若点![]() 恰好落在
恰好落在![]() 上,求
上,求![]() 的值;
的值;
(3)点E在![]() 边上运动的过程中,
边上运动的过程中,![]() 的度数是否存在最大值,若存在,求出此时线段
的度数是否存在最大值,若存在,求出此时线段![]() 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
【答案】(1)证明见解析,(2)![]() =
=![]() ,(3)
,(3)![]() 的度数是最大值为90°,此时线段
的度数是最大值为90°,此时线段![]() 的长=
的长=![]() .
.
【解析】
![]() 由折叠知∠AEB=∠A’EB,再利矩形性质可得
由折叠知∠AEB=∠A’EB,再利矩形性质可得![]() ,结合直角三角形两锐角互余即可得出结论;
,结合直角三角形两锐角互余即可得出结论;![]() 先由矩形性质结合勾股定理求得
先由矩形性质结合勾股定理求得![]() ,由折叠性质用勾股定理建立方程求解即可求出AE的长,进而求出结论;
,由折叠性质用勾股定理建立方程求解即可求出AE的长,进而求出结论;![]() 先判断出∠A’CB最大时,点
先判断出∠A’CB最大时,点![]() 在CE上,进而利用三角形的面积求出CE,进而用勾股定理求出DE,即可得出结论.
在CE上,进而利用三角形的面积求出CE,进而用勾股定理求出DE,即可得出结论.
解:![]() 由折叠知∠AEB=∠A’EB,
由折叠知∠AEB=∠A’EB,
∴∠AEB=![]() =
=![]() ,
,![]() 四边形ABCD是矩形,
四边形ABCD是矩形,![]() ,
,
∴![]() =
=![]() =
=![]() ,
,
∴![]() =2∠ABE;
=2∠ABE;![]() 四边形ABCD是矩形,
四边形ABCD是矩形,![]() ,
,![]() ,
,
在![]() 中,根据勾股定理得,
中,根据勾股定理得,![]() ,
,
设![]() ,
,![]() ,
,
由折叠知,![]() ,
,![]() ,
,![]() ,
,![]() =BD-
=BD-![]() =4,
=4,
∴∠DA’E=90°,
在![]() 中,根据勾股定理得,
中,根据勾股定理得,![]() =16,
=16,![]() ,
,![]() ,
,![]() ,
,
在![]() 中,
中,![]() ;
;![]() 的度数是存在最大值,
的度数是存在最大值,
理由:如图1,过点B作![]() 交
交![]() 的延长线于F,
的延长线于F,
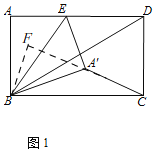
在![]() 中,
中,![]() ,
,![]() 越大时,
越大时,![]() 越大,即
越大,即![]() 越大,
越大,
当点E在边AD上运动时,点![]() 与F重合时,BF最大=A’B=AB=6,
与F重合时,BF最大=A’B=AB=6,
∴A’B⊥A’C,
∴![]() ,
,
由折叠知,![]() ,
,![]() 点
点![]() 在CE上,如备用图,
在CE上,如备用图,
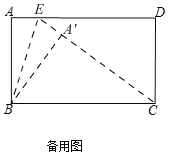
![]() 四边形ABCD是矩形,
四边形ABCD是矩形,![]() ,
,![]() ,
,
根据三角形面积得:![]() =
=![]() ,
,
∴A’B=AB,![]() ,
,
在![]() 中,根据勾股定理
中,根据勾股定理![]() ,
,![]() .
.

 阅读快车系列答案
阅读快车系列答案【题目】在星期一的第八节课,我校体育老师随机抽取了九年级的总分学生进行体育中考的模拟测试,并对成绩进行统计分析,绘制了频数分布表和统计图,按得分划分成A、B、C、D、E、F六个等级,并绘制成如下两幅不完整的统计图表.
等级 | 得分x(分) | 频数(人) |
A | 95<x≤100 | 4 |
B | 90<x≤95 | m |
C | 85<x≤90 | n |
D | 80<x≤85 | 24 |
E | 75<x≤80 | 8 |
F | 70<x≤75 | 4 |
请你根据图表中的信息完成下列问题:
1)本次抽样调查的样本容量是 .其中m= ,n= .
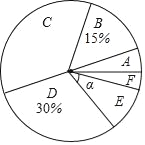
2)扇形统计图中,求E等级对应扇形的圆心角α的度数;
3)我校九年级共有700名学生,估计体育测试成绩在A、B两个等级的人数共有多少人?
4)我校决定从本次抽取的A等级学生(记为甲、乙、丙、丁)中,随机选择2名成为学校代表参加全市体能竞赛,请你用列表法或画树状图的方法,求恰好抽到甲和乙的概率.