Question

【题目】已知关于x的一元二次方程|x2﹣1|＝（x﹣1）（kx﹣2）：

（1）若k＝3，求方程的解；

（2）若方程恰有两个不同解，求实数k的取值范围．

Answer 1

【答案】（1）x1＝，x2＝1，x3＝；（2）k≤0或k＝1或k≥4．

【解析】

（1）将k＝3代入原方程，然后根据绝对值的性质把原方程化成两个一元二次方程进行解答；

（2）由于x＝1恒为方程|x21|＝（x1）（kx2）的解，当x≠1时，只需函数y＝与函数y＝kx2的图象只有一个交点就可以，画出x≠1时函数y＝，根据图象确定直线y＝kx2与函数y＝图象只有一个交点时，k的取值范围便可．

解：（1）把k＝3代入|x2﹣1|＝（x﹣1）（kx﹣2）中，得|x2﹣1|＝（x﹣1）（3x﹣2），

当x2＞1，即x＞1或x＜﹣1时，原方程可化为：x2﹣1＝（x﹣1）（3x﹣2），

解得，x＝1（舍），或x＝；

当x2≤1，即﹣1≤x≤1时，原方程可化为：1﹣x2＝（x﹣1）（3x﹣2），

解得，x＝1，或x＝；

综上，方程的解为x1＝，x2＝1，x3＝；

（2）∵x＝1恒为方程|x2﹣1|＝（x﹣1）（kx﹣2）的解，

∴当x≠1时，方程两边都同时除以x﹣1得，=kx﹣2，

要使此方程只有一个解，只需函数y＝与函数y＝kx﹣2的图象只有一个交点．

∵函数：，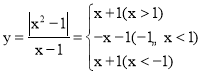

作出函数图象，

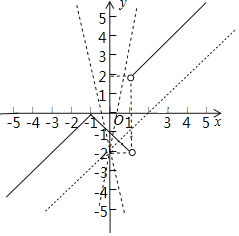
由图象可知，当k＜0时，直线y＝kx﹣2与函数y＝图象只有一个交点；

当k＝0时，直线y＝kx﹣2＝﹣2与函数y图象只有一个交点；

当k＝1时，y＝kx﹣2＝x﹣2与y＝x+1平行，则与函数y＝图象只有一个交点；

∵当直线y＝kx﹣2过（1，2）点时，2＝k﹣2，则k＝4，

∴函数图象可知，当k≥4时，直线y＝kx﹣2与函数y＝图象也只有一个交点，

∴要使函数图象与y＝kx﹣2图象有且只有一个交点，则实数k的取值范围是k≤0或k＝1或k≥4．

综上，实数k的取值范围：k≤0或k＝1或k≥4．