题目内容
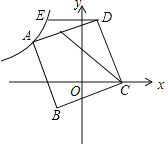
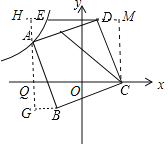
【题目】如图,在平面直角坐标系中,正方形ABCD顶点B(﹣1,﹣1),C在x轴正半轴上,A在第二象限双曲线y=﹣![]() 上,过D作DE∥x轴交双曲线于E,连接CE,则△CDE的面积为( )
上,过D作DE∥x轴交双曲线于E,连接CE,则△CDE的面积为( )
A.3B.![]() C.4D.
C.4D.![]()
【答案】B
【解析】
作辅助线,构建全等三角形:过A作GH⊥x轴,过B作BG⊥GH,过C作CM⊥ED于M,证明△AHD≌△DMC≌△BGA,设A(x,﹣![]() ),结合点B 的坐标表示:BG=AH=DM=﹣1﹣x,由HQ=CM,列方程,可得x的值,进而根据三角形面积公式可得结论.
),结合点B 的坐标表示:BG=AH=DM=﹣1﹣x,由HQ=CM,列方程,可得x的值,进而根据三角形面积公式可得结论.
过A作GH⊥x轴,过B作BG⊥GH,过C作CM⊥ED于M,
设A(x,﹣![]() ),
),
∵四边形ABCD是正方形,
∴AD=CD=AB,∠BAD=∠ADC=90°,
∴∠BAG=∠ADH=∠DCM,
∴△AHD≌△DMC≌△BGA(AAS),
∴BG=AH=DM=﹣1﹣x,
∴AG=CM=DH=1﹣![]() ,
,
∵AH+AQ=CM,
∴1﹣![]() =﹣
=﹣![]() ﹣1﹣x,
﹣1﹣x,
解得:x=﹣2,
∴A(﹣2,2),CM=AG=DH=1﹣![]() =3,
=3,
∵BG=AH=DM=﹣1﹣x=1,
∴点E的纵坐标为3,
把y=3代入y=﹣![]() 得:x=﹣
得:x=﹣![]() ,
,
∴E(﹣![]() ,3),
,3),
∴EH=2﹣![]() =
=![]() ,
,
∴DE=DH﹣HE=3﹣![]() =
=![]() ,
,
∴S△CDE=![]() DECM=
DECM=![]() ×
×![]() ×3=
×3=![]() .
.
故选:B.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目