题目内容
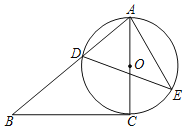
【题目】如图,抛物线![]() 与
与![]() 轴相交于点
轴相交于点![]() 、
、![]() ,与
,与![]() 轴相交于点
轴相交于点![]() ,过点
,过点![]() 作
作![]() ,与抛物线相交于点
,与抛物线相交于点![]() .点
.点![]() 从点
从点![]() 出发,在折线段
出发,在折线段![]() 上以每秒2个单位长度向終点
上以每秒2个单位长度向終点![]() 勾速运动,点
勾速运动,点![]() 从点
从点![]() 出发,在线段
出发,在线段![]() 上以每秒1个单位长度向终点
上以每秒1个单位长度向终点![]() 匀速运动,两点同时出发,当其中一个点到达终点时,另一个点也停止运动,连接
匀速运动,两点同时出发,当其中一个点到达终点时,另一个点也停止运动,连接![]() .设点
.设点![]() 的运动时间为
的运动时间为![]() ,线段
,线段![]() 的长度的平方为
的长度的平方为![]() ,即
,即![]() (单位长度
(单位长度![]() ),
),
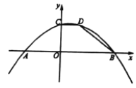
(1)求线段![]() 的长;
的长;
(2)求![]() 关于
关于![]() 的函数解析式,并直接写出自变量
的函数解析式,并直接写出自变量![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2) .
.
【解析】
(1)先求出点B、C、D的坐标,过点![]() 作
作![]() 轴于点
轴于点![]() ,得到DE=3,BE=4,由勾股定理求出BD=5;
,得到DE=3,BE=4,由勾股定理求出BD=5;
(2)分两种情况:当![]() 时,过点
时,过点![]() 作
作![]() 轴于点
轴于点![]() ,由BQ=t,BP=2t得到
,由BQ=t,BP=2t得到![]() ,
,![]() ,求出
,求出![]() ,利用勾股定理即可求出d;当
,利用勾股定理即可求出d;当![]() 时,过点
时,过点![]() 作
作![]() 轴于点
轴于点![]() ,证明四边形
,证明四边形![]() 是矩形,利用矩形的性质求出
是矩形,利用矩形的性质求出![]() ,
,![]() ,再根据勾股定理求出d.
,再根据勾股定理求出d.
(1)当![]() 时,
时,![]() ,解得
,解得![]() ,
,![]() .
.
当![]() 时,
时,![]() ,解得
,解得![]() ,
,![]() .
.
当![]() 时,则
时,则![]() .
.
所以点![]() ,点
,点![]() ,点
,点![]() .
.
过点![]() 作
作![]() 轴于点
轴于点![]() ,如图1.则
,如图1.则![]() ,
,![]() ,BE=6-2=4.
,BE=6-2=4.
![]() .
.
(2)如图1,当![]() 时,过点
时,过点![]() 作
作![]() 轴于点
轴于点![]() ,则
,则![]() .
.
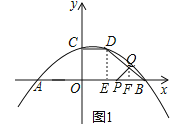
由(1)得,![]() ,
,![]() .
.
∵BQ=t,BP=2t,
∴![]() ,
,![]() .
.
![]() .
.
![]() .
.
如图2,当![]() 时,过点
时,过点![]() 作
作![]() 轴于点
轴于点![]() ,则
,则![]() .
.
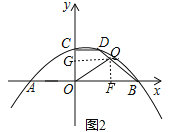
![]() 四边形
四边形![]() 是矩形.
是矩形.
![]() ,
,![]() .
.
![]() ,
,![]() .
.
![]() .
.
综上,d= 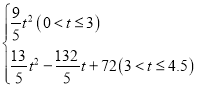 .
.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目