题目内容
【题目】在△ABC中,∠ACB=90,AC=BC=1,E、F为线段AB上两动点,且∠ECF=45°,过点E、F分别作BC、AC的垂线相交于点M,垂足分别为H、G.现有以下结论:
①AB=![]() ; ②当点E与点B重合时,MH=
; ②当点E与点B重合时,MH=![]() ; ③AF+BE=EF;④F、E分别不与端点A、B重合时,总有S△AGF+ S△EBH= S△FEM,其中正确结论为--------------------------( )
; ③AF+BE=EF;④F、E分别不与端点A、B重合时,总有S△AGF+ S△EBH= S△FEM,其中正确结论为--------------------------( )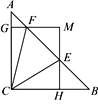
A. ①②③ B. ①②④ C. ①③④ D. ①②③④
【答案】B
【解析】(1)∵在△ABC中,∠ACB=90,AC=BC=1,
∴AB=![]() ,故①正确;
,故①正确;
(2)如下图1,当点E与点B重合时,点H与点B重合,
∴MB⊥BC,∠MBC=90°,
∵MG⊥AC,
∴∠MGC=∠C=∠MBC=90°,
∴MG∥BC,四边形MGCB是矩形,
∴MH=MB=CG,
∵∠FCE=45°=∠ABC,∠A=45°=∠ACF,
∴AF=CF=BF,
∴FG是△ACB的中位线,
∴GC=![]() AC=
AC=![]() ,
,
∴MH=GC=![]() ,故②正确;
,故②正确;
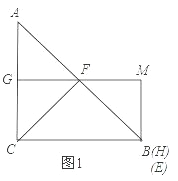
(3)如下图2所示,
∵AC=BC,∠ACB=90°,
∴∠A=∠5=45°.
将△ACF顺时针旋转90°至△BCD,则CF=CD,∠1=∠4,∠A=∠6=45°,BD=AF;
∵∠2=45°,
∴∠1+∠3=∠3+∠4=45°,
∴∠DCE=∠2,
∵在△ECF和△ECD中,CF=CD,∠2=∠DCE,CE=CE,
∴△ECF≌△ECD(SAS),
∴EF=DE,
∵∠5=45°,
∴∠BDE=90°,
∴DE2=BD2+BE2,即EF2=AF2+BE2,故③错误;
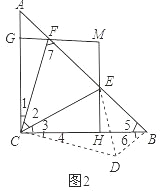
(4)∵△ABC中,∠ACB=90°,AC=BC,
∴∠A=∠B=45°,
∵MG⊥AC,MH⊥BC,
∴∠AGF=∠BHE=90°,
∴∠AFG=∠BEH=45°,
∴∠MFE=∠AFG=45°,∠MEF=∠BEH=45°,
∴△AGF、△BEH、△MEF都是等腰直角三角形,
∴AG=FG=![]() AF,BH=HE=
AF,BH=HE=![]() BE,ME=MF=
BE,ME=MF=![]() EF,
EF,
∴S△AGF=![]() AF2,S△BEH=
AF2,S△BEH=![]() BE2,S△MEF=
BE2,S△MEF=![]() EF2,
EF2,
∵EF2=AF2+BE2,
∴S△AGF+S△BEH=S△MEF,故④正确.
综上所述,正确的结论是①②④.
故选B.

 步步高达标卷系列答案
步步高达标卷系列答案




