题目内容
【题目】如图①，在正方形ABCD中，点P沿边DA从点D开始向点A以1cm/s的速度移动；同时，点Q沿边AB、BC从点A开始向点C以2cm/s的速度移动．当点P移动到点A时，P、Q同时停止移动．设点P出发xs时，△PAQ的面积为ycm2 ， y与x的函数图象如图②，则线段EF所在的直线对应的函数关系式为 ． 
【答案】y=﹣3x+18
【解析】解：∵点P沿边DA从点D开始向点A以1cm/s的速度移动；点Q沿边AB、BC从点A开始向点C以2cm/s的速度移动．
∴当Q到达B点，P在AD的中点时，△PAQ的面积最大是9cm2 ， 设正方形的边长为acm，
∴ 
× a×a=9，
解得a=6，即正方形的边长为6，
当Q点在BC上时，AP=6﹣x，△APQ的高为AB，
∴y= （6﹣x）×6，即y=﹣3x+18．
故答案为：y=﹣3x+18．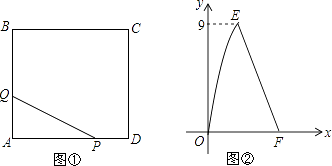
根据从图②可以看出当Q点到B点时的面积为9，求出正方形的边长，再利用三角形的面积公式得出EF所在的直线对应的函数关系式．
练习册系列答案
相关题目
