题目内容
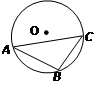
(1)如图①,PA、PB分别与⊙O相切于点A、B.求证:PA=PB.
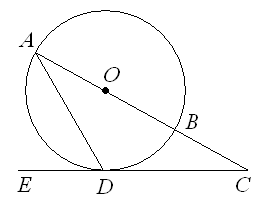
(2)如图②,过⊙O外一点P的两条直线分别与⊙O相交于点A、B和C、D.
则当 时,PB=PD
(不添加字母符号和辅助线,不需证明,只需填上符合题意的一个条件).

(2)如图②,过⊙O外一点P的两条直线分别与⊙O相交于点A、B和C、D.
则当 时,PB=PD
(不添加字母符号和辅助线,不需证明,只需填上符合题意的一个条件).

.证明:⑴ 连接OA,OB,
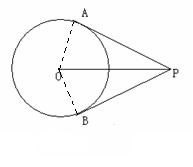
∵PA,PB分别是⊙O的切线,
∴OA⊥PA,OB⊥PB ┄┄2′
在Rt△POA和Rt△POB中,
∵ ┄┄3′
┄┄3′
∴Rt△POA≌Rt△POB┄┄4′
∴PA=PB┄┄5′
⑵ AB=CD ┄┄7′

∵PA,PB分别是⊙O的切线,
∴OA⊥PA,OB⊥PB ┄┄2′
在Rt△POA和Rt△POB中,
∵
 ┄┄3′
┄┄3′∴Rt△POA≌Rt△POB┄┄4′
∴PA=PB┄┄5′
⑵ AB=CD ┄┄7′
略

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 和⊙
和⊙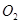 的半径分别是12和2,圆心
的半径分别是12和2,圆心 。”那么,据此你判断儿子打球所用的时间应是()
。”那么,据此你判断儿子打球所用的时间应是()
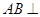 半径
半径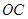 于
于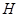 ,
,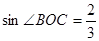 ,则
,则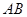 的长度为( )
的长度为( )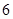

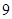
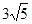
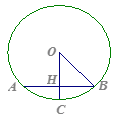

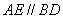 ,∠1=130o,∠2=30o,则∠C= .
,∠1=130o,∠2=30o,则∠C= . 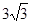 ,求BC的长.
,求BC的长.