题目内容
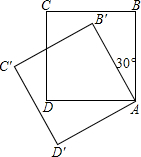如图，将边长为1的正方形ABCD绕A点按逆时针方向旋转30°，至正方形AB′C′D′，则旋转前后正方形重叠部分的面积是分析：设CD，B′C′相交于点M，DM=x，则∠MAD=30°，AM=2x，x2+1=4x2，解得x=
，所以重叠部分的面积SADMB′=
．
| ||
| 3 |
| ||
| 3 |
解答：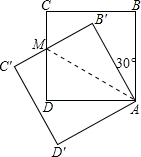
解：设CD，B′C′相交于点M，DM=x，则∠MAD=30° AM=2x，
∵x2+1=4x2，
∴x=
，
∴重叠部分的面积SADMB′=
×1=
．
解：设CD，B′C′相交于点M，DM=x，则∠MAD=30° AM=2x，∵x2+1=4x2，
∴x=
| ||
| 3 |
∴重叠部分的面积SADMB′=
| ||
| 3 |
| ||
| 3 |
点评：本题考查旋转的性质．旋转变化前后，对应点到旋转中心的距离相等以及每一对对应点与旋转中心连线所构成的旋转角相等．要注意旋转的三要素：①定点-旋转中心；②旋转方向；③旋转角度．
练习册系列答案
相关题目
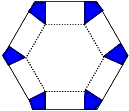如图，将边长为6cm的正六边形纸板的六个角各剪切去一个全等的四边形，再沿虚线折起，做成一个无盖直六棱柱纸盒，使侧面积等于底面积，被剪去的六个四边形的面积和为如图，将边长为a的正六边形A1A2A3A4A5A6在直线l上由图1的位置按顺时针方向向右作无滑动滚动，当A1第一次滚动到图2位置时，顶点A1所经过的路径的长为（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
（2013•丰南区一模）如图，将边长为a的正六边形A1A2A3A4A5A6在直线l上由图1的位置按顺时针方向向右作无滑动滚动，当A1第一次滚动到图2位置时，顶点A1所经过的路径的长为