题目内容
如果一条抛物线 与
与 轴有两个交点,那么以该抛物线的顶点和这两个交点为顶点的三角形称为这条抛物线的“抛物线三角形”.
轴有两个交点,那么以该抛物线的顶点和这两个交点为顶点的三角形称为这条抛物线的“抛物线三角形”.
(1)“抛物线三角形”一定是 三角形;
(2)如图,△OAB是抛物线 的“抛物线三角形”,是否存在以原点O为对称中心的矩形ABCD?若存在,求出过O、C、D三点的抛物线的表达式;若不存在,说明理由;
的“抛物线三角形”,是否存在以原点O为对称中心的矩形ABCD?若存在,求出过O、C、D三点的抛物线的表达式;若不存在,说明理由;
(3)在(2)的条件下,若以点E为圆心,r为半径的圆与线段AD只有一个公共点,求出r的取值范围.
(1)等腰;(2)存在,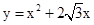 ;(3)
;(3) 或
或 .
.
解析试题分析:(1)根据抛物线的轴对称性和等腰三角形的判定可得结论.
(2)根据“抛物线三角形”求出A,B的坐标,求出A,B关于原点O为对称的点C,D的坐标,根据待定系数法求出过O、C、D三点的抛物线的表达式.
(3)点E为圆心,r为半径的圆与线段AD只有一个公共点,则⊙E与AD相切或⊙E的半径在AE和AD之间.
(1)等腰 .
(2)存在.
如图,作△OCD与△OAB关于原点O中心对称,则四边形ABCD为平行四边形.
当OA=OB时,平行四边形ABCD为矩形 .
又∵AO=AB,∴△OAB为等边三角形.
作AE⊥OB,垂足为E.
∴ .∴
.∴ (b﹥0).∴
(b﹥0).∴ .
.
∴ .
.
∴ .
.
设过点O,C,D三点的抛物线 ,则
,则 ,解之,得
,解之,得 .
.
∴所求抛物线的表达式为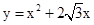 .
.
(3)①⊙E与AD相切时, .
.
②⊙E过点D时, .
.
③⊙E过点A时,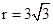 .
.
综上所述, 或
或 .
.
考点:1.新定义;2.二次函数的性质;3.等腰三角形的判定;4.关于坐标原点对称的性质;5.待定系数法的应用;6.曲线上点的坐标与方程的关系;7.直线与圆的位置关系;8.分类思想的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 与x轴交点为A、B(点B在点A的右侧),与y轴交于点C.
与x轴交点为A、B(点B在点A的右侧),与y轴交于点C. 是等腰三角形,求抛物线的解析式;
是等腰三角形,求抛物线的解析式; ,点P(n,0)是x轴上一个动点,在(2)的条件下,过点P作垂直于x轴的直线交这个一次函数的图象于点M,交抛物线
,点P(n,0)是x轴上一个动点,在(2)的条件下,过点P作垂直于x轴的直线交这个一次函数的图象于点M,交抛物线 时,点M位于点N的下方,求这个一次函数的解析式.
时,点M位于点N的下方,求这个一次函数的解析式.
 与x轴的交点为A、D(A在D的右侧),与y轴的交点为C.
与x轴的交点为A、D(A在D的右侧),与y轴的交点为C.


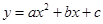 交
交 轴于A、B两点(点A在点B左侧),与
轴于A、B两点(点A在点B左侧),与 轴交于点C,点A、C的坐标分别为(-3,0),(0,3),对称轴直线
轴交于点C,点A、C的坐标分别为(-3,0),(0,3),对称轴直线 交
交 ,,求点P的坐标;
,,求点P的坐标;

