Question

如图，在直角坐标系中，已知直线y=kx+6与x轴、y轴分别交于A、B两点，且△ABO的面积为12．

【小题1】（1）求k的值；
【小题2】（2）若P为直线AB上一动点，P点运动到什么位置时，△PAO是以OA为底的等腰三角形，求点P的坐标；
【小题3】（3）在（2）的条件下，连结PO，△PBO是等腰三角形吗？如果是，试说明理由，如果不是，请在线段AB上求一点C，使得△CBO是等腰三角形．

Answer 1

【小题1】．解：（1）∵y=kx+6，∴B(0，6)，∴OB=6．
又S_△ABO=12，∴OA=4，∴A（-4，0）．
把A(-4，0)代入y=kx+6，
即-4k+6=0，解得k=．
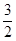【小题2】（2）过OA的中点作OA的垂线交直线AB于P，则x_P=-2，
把x_P=-2代入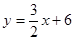，得．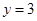
∴P(-2，3)．
【小题3】（3）解法一∵△APO是等腰三角形，
∴∠PAO=∠POA．
∵∠PAO+∠ABO=90º，∠POA+∠POB=90º，
∴∠ABO=∠POB．
∴△POB是等腰三角形．         ………………5分
解法二：∵P(-2，3)，OB=6，
∴P是OB中垂线上的一点．
∴PB=PO．解析:
略