Question

【题目】先阅读下面的知识，后解答后面的问题：

探究：如图，在△ABC中，已知∠B=∠C，求证：AB=AC.

证明：过点A作AD⊥BC，垂足为D, 在△ABD与△ACD中，

∠B=∠C， , , 所以△ABD≌△ACD（ ），所以AB=AC.

（1）完成上述证明中的空白；

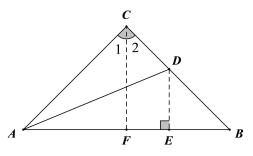
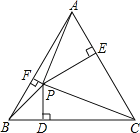
（2）已知如图，在△ABC中，AC=BC，∠ACB=90°，AD平分∠CAB.试问：AC+CD与AB相等吗？说明理由.

Answer 1

【答案】（1），AD=AD，AAS；（2）AC+CD=AB，理由见解析.

【解析】

（1）根据AAS可判定△ABD≌△ACD，进而完成填空；

（2）过点D作DE⊥AB，垂足为E，如图，先用AAS证明△ACD≌△AED，得到AC=AE，再作∠ACB的平分线CF交AB于点F，利用SAS证明△ACF≌△BCF，得到∠CAB=∠B，进一步通过三角形的内角和得出∠DEB=∠B，进而根据探究结论推出ED=EB，即可证得结论.

解：（1）证明：过点A作AD⊥BC，垂足为D, 在△ABD与△ACD中，

∠B=∠C， ， AD=AD ，

所以△ABD≌△ACD（AAS），

所以AB=AC.

故答案为：，AD=AD，AAS.

（2）AC+CD=AB，理由如下：

过点D作DE⊥AB，垂足为E，如图，则∠AED=90°，

∵∠ACB=90°，∴∠ACB=∠AED，

∵AD平分∠CAB，∴∠CAD=∠EAD，

在△ACD和△AED中，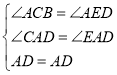

∴△ACD≌△AED（AAS）.

∴AC=AE，CD=ED，

作∠ACB的平分线CF交AB于点F，则∠1=∠2，

在△ACF和△BCF中，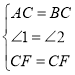

∴△ACF≌△BCF（SAS），∴∠CAB=∠B，

∵∠ACB=90°，∴∠CAB=∠B=45°，

∴∠DEB=90°－∠B=45°，

∴∠DEB=∠B，

由探究结论知：ED=EB.

∴BE=CD，

∴AB=AE+BE=AC+CD.