题目内容
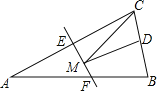
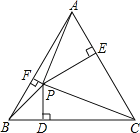
【题目】如图，P为边长为2的等边三角形ABC内任意一点，连接PA、PB、PC，过P点分别作BC、AC、AB边的垂线，垂足分别为D、E、F，则PD+PE+PF等于（ ）
A.
B.
C.2D.
【答案】B
【解析】
求出等边三角形的高，再根据△ABC的面积等于△PAB、△PBC、△PAC三个三角形面积的和，列式并整理即可得到PD＋PE＋PF等于三角形的高．
解：∵正三角形的边长为2，
∴高为2×sin60°＝
，
∴S△ABC＝
×2×＝，
∵PD、PE、PF分别为BC、AC、AB边上的高，
∴S△PBC＝BCPD，S△PAC＝ACPE，S△PAB＝ABPF，
∵AB＝BC＝AC，
∴S△PBC+S△PAC+S△PAB＝BCPD+ACPE+ABPF＝×2（PD+PE+PF）＝PD+PE+PF，
∵S△ABC＝S△PBC+S△PAC+S△PAB，
∴PD+PE+PF＝．
故选：B．
练习册系列答案
相关题目
