题目内容
【题目】抛物线y＝－x2＋2x＋3与x轴交于点A、B(点A在点B的左侧)，与y轴交于点C.
(1)求直线BC的表达式；
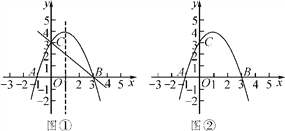
(2)抛物线的对称轴上存在点P，使∠APB＝∠ABC，利用图①求点P的坐标；
(3)点Q在y轴右侧的抛物线上，利用图②比较∠OCQ与∠OCA的大小，并说明理由．
【答案】（1）y＝－x＋3（2）P点的坐标为(1，2＋2
)或(1，－2－2
)（3）当Q点的横坐标为5时，∠OCA＝∠OCQ；当Q点的横坐标大于5时，则∠OCQ逐渐变小，故∠OCA＞∠OCQ；当Q点的横坐标小于5且大于0时，则∠OCQ逐渐变大，故∠OCA＜∠OCQ.
【解析】试题分析：（1）由抛物线解析式可求B、C的坐标，利用待定系数法可求直线BC的解析式；
（2）由直线BC的解析式可知∠APB=∠ABC=45°，设抛物线对称轴交直线BC于点D，交x轴于点E，结合二次函数的对称性可得PB=PD，根据勾股定理求出BD的长，从而求出PE的长，进而求出P的坐标；
（3）设Q（x，－x2＋2x＋3），当∠OCA=∠OCQ时，利用三角形相似可得到关于x的方程，求出Q点的横坐标，再结合图形比较两角的大小.
试题解析：(1)在y＝－x2＋2x＋3中，令y＝0可得0＝－x2＋2x＋3，解得x＝－1或x＝3，令x＝0可得y＝3，∴B(3，0)，C(0，3)．∴可设直线BC的表达式为y＝kx＋3，把B点坐标代入可得3k＋3＝0，解得k＝－1，∴直线BC的表达式为y＝－x＋3.
(2)∵OB＝OC，∴∠ABC＝45°.∵y＝－x2＋2x＋3＝－(x－1)2＋4，∴抛物线的对称轴为直线x＝1.
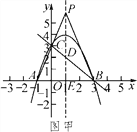
设抛物线的对称轴交直线BC于点D，交x轴于点E，当点P在x轴上方时，如图甲，∵∠APB＝∠ABC＝45°，且PA＝PB，∴∠PBA＝67.5°，∠DPB＝
∠APB＝22.5°，∴∠PBD＝22.5°，∴∠DPB＝∠DBP，∴DP＝DB.在Rt△BDE中，BE＝DE＝2，∴BD＝2
，∴PE＝2＋2
，∴P(1，2＋2
)；
当点P在x轴下方时，由对称性可知P点坐标为(1，－2－2
)．
综上可知，P点的坐标为(1，2＋2
)或(1，－2－2
)．
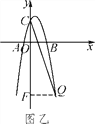
(3)设Q(x，－x2＋2x＋3)，当点Q在x轴下方时，如图乙，过点Q作QF⊥y轴于点F，则CF＝x2－2x.当∠OCA＝∠OCQ时，则△QFC∽△AOC，∴
，即
，解得x＝0(舍去)或x＝5.
∴当Q点的横坐标为5时，∠OCA＝∠OCQ；当Q点的横坐标大于5时，则∠OCQ逐渐变小，故∠OCA＞∠OCQ；当Q点的横坐标小于5且大于0时，则∠OCQ逐渐变大，故∠OCA＜∠OCQ.
