��Ŀ����
����Ŀ�����Ķ����н����̣�Ȼ���ٽ��⣮
������֪����ʽ2x3��x2+m��һ����ʽ��2x+1����m��ֵ��
�ⷨһ����2x3��x2+m����2x+1����x 2+ax+b����
��2x 3��x2+m��2x 3+��2a+1��x2+��a+2b��x+b��
�Ƚ�ϵ����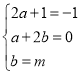 �����
�����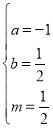 ����m��
����m��![]() ��
��
�ⷨ������2x3��x2+m��A��2x+1����AΪ��ʽ��
������ʽΪ���ʽ��Ϊ���������ȡx����![]() ��2��������3��������2+m��0����m��
��2��������3��������2+m��0����m��![]() ��
��
��1����֪����ʽ2x3��2x2+ m��һ����ʽ��x+2����m��ֵ��
��2����֪x 4+ m x3+ n x��16����ʽ��x��1���ͣ�x��2������m��n��ֵ��
���𰸡���1��m��24����2��m����5��n��20��
��������
��1����2x3��2x2+m��A��x+2����AΪ��ʽ���������Ǻ��ʽ����ȡx=-2�����뼴�ɽ��
��2����x4+mx3+nx��16��A��x��1����x��2����AΪ��ʽ���������Ǻ��ʽ����ȡx=1��x=2�����뼴�ɽ��
�⣺��1���߶���ʽ2x3��2x2+m��һ����ʽ��x+2��
����2x3��2x2+m��A��x+2����AΪ��ʽ��
������ʽΪ���ʽ��Ϊ�������ȡx����2��
2������2��3��2������2��2+m��0����m��24��
��2����x4+mx3+nx��16����ʽ��x��1���ͣ�x��2����
����x4+mx3+nx��16��A��x��1����x��2����AΪ��ʽ��
������ʽΪ���ʽ��Ϊ�������ȡx��2��x��1��
����ã�24+m��23+2n��16��0��14+m��13+n��16��0��
��ã�m����5��n��20��