题目内容
某风景区的湖心岛靠水边有一凉亭A,其正东方向的湖边B处有一棵大树,游客李先生必须在10分钟之内从湖心岛凉亭A处划船赶回湖边B,否则
他将赶不上旅游车约定的发车时间.已知湖边建筑物C在凉亭A的南偏东45°方向上,也在大树B的南偏西32°的方向上,且量得B、C间的距离为100m.若
李先生立即登船以15m/s的速度划行,问他能否在规定时间内赶到B处?
(参考数据:sin32°=0.5299 cos32°=0.8480)
他将赶不上旅游车约定的发车时间.已知湖边建筑物C在凉亭A的南偏东45°方向上,也在大树B的南偏西32°的方向上,且量得B、C间的距离为100m.若
李先生立即登船以15m/s的速度划行,问他能否在规定时间内赶到B处?
(参考数据:sin32°=0.5299 cos32°=0.8480)

能在规定时间内赶到B处。
分析:过点C作正北线交AB于点D,则在图中有两个直角三角形。先在RT△BCD中,通过BC,以及∠DCB求出CD和BD。再把CD放到RT△ACD中,借助于∠ACD求出AD,最后把AD和BD相加即可。

解答:过点C作正北线交AB于点D.
∵BC=100m,
∴在Rt△CBD中,BD=BC?sin32°=100×0.5299=52.99(m).
DC=BC?cos∠DCB=100?cos32°=100×0.8480=84.80(m).
在Rt△ADC中,tan∠ACD=ADCD
AD=CD?tan∠ACD=84.80×tan45°=84.80(m).
AB=AD+DB=84.80+52.99≈138(m).
因为138÷15<10,
所以能在规定时间内赶到B处。

练习册系列答案
相关题目


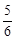 ,求AE的值.
,求AE的值.

 +(1-tanB)2=0,求∠C的度数
+(1-tanB)2=0,求∠C的度数 ,则坡角
,则坡角 为 度
为 度
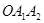 =∠
=∠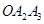 =∠
=∠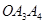 =…=90°,
=…=90°,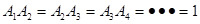
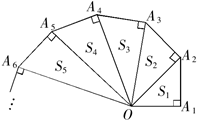
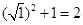 ,
,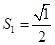 ;
;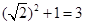 ,
,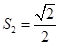 ;
;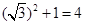 ,
,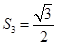 ,……
,…… .
.