题目内容
如图,四边形ABCD是平行四边形,以AB为直径的
⊙O经过点D,E是⊙O上一点,且ÐAED=45°.

小题1: (1) 试判断CD与⊙O的位置关系,并证明你的结论;
小题2:(2) 若⊙O的半径为3,sinÐADE=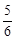 ,求AE的值.
,求AE的值.
⊙O经过点D,E是⊙O上一点,且ÐAED=45°.

小题1: (1) 试判断CD与⊙O的位置关系,并证明你的结论;
小题2:(2) 若⊙O的半径为3,sinÐADE=
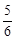 ,求AE的值.
,求AE的值.小题1:(1)CD与圆O相切. …………………1分
证明:连接OD,则ÐAOD=2ÐAED =2´45°=90°. …………………2分
∵四边形ABCD是平行四边形,
∴AB//DC.
∴ÐCDO=ÐAOD=90°.
∴OD^CD. …………………3分
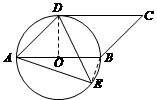 ∴CD与圆O相切
∴CD与圆O相切小题2:(2)连接BE,则ÐADE=ÐABE.
∴sinÐADE=sinÐABE=
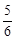 . …………………4分
. …………………4分∵AB是圆O的直径,
∴ÐAEB=90°,AB=2´3=6.
在Rt△ABE中,sinÐABE=
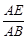 =
=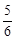 .
. ∴AE="5" .
略

练习册系列答案
相关题目
 的
的 .
.



 )
) 中,
中, ,
, ,
, ,则
,则 的长为( )
的长为( )




 ≈1.414,
≈1.414, ≈1.732).
≈1.732).


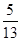



 ,那么∠A 取值范围是 ( )
,那么∠A 取值范围是 ( )