ЬтФПФкШн
ЁОЬтФПЁПЖдгкЦНУцжБНЧзјБъЯЕжаЕФШЮвтСНЕуP1ЃЈx1ЃЌy1ЃЉЃЌP2ЃЈx2ЃЌy2ЃЉЃЌЮвУЧАб![]() НазіP1ЁЂP2СНЕуМфЕФжБНЧОрРыЃЌМЧзїdЃЈP1ЃЌP2ЃЉЃЎ
НазіP1ЁЂP2СНЕуМфЕФжБНЧОрРыЃЌМЧзїdЃЈP1ЃЌP2ЃЉЃЎ
ЃЈ1ЃЉвбжЊOЮЊзјБъдЕуЃЌЖЏЕуPЃЈxЃЌyЃЉТњзуdЃЈOЃЌPЃЉ=1ЃЌЧыаДГіxгыyжЎМфТњзуЕФЙиЯЕЪНЃЌВЂдкЫљИјЕФжБНЧзјБъЯЕжаЛГіЫљгаЗћКЯЬѕМўЕФЕуPЫљзщГЩЕФЭМаЮЃЛ
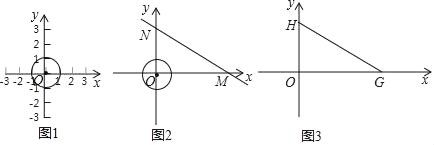
ЃЈ2ЃЉЩшP0ЃЈx0ЃЌy0ЃЉЪЧвЛЖЈЕуЃЌQЃЈxЃЌyЃЉЪЧжБЯпy=ax+bЩЯЕФЖЏЕуЃЌЮвУЧАбdЃЈP0ЃЌQЃЉЕФзюаЁжЕНазіP0ЕНжБЯпy=ax+bЕФжБНЧОрРыЃЎЪдЧѓЕуMЃЈ2ЃЌ1ЃЉЕНжБЯпy=x+2ЕФжБНЧОрРыЃЎ
ЁОД№АИЁПЃЈ1ЃЉ|x|+|y|=1ЃЌЛЭММћНтЮіЃЛЃЈ2ЃЉ3
ЁОНтЮіЁПЪдЬтЗжЮіЃКЃЈ1ЃЉИљОнаТЖЈвхжЊ|x|+|y|=1ЃЌОнДЫПЩвдЛГіЗћКЯЬтвтЕФЭМаЮ.
ЃЈ2ЃЉИљОнаТЖЈвхжЊdЃЈMЃЌQЃЉ=|xЉ2|+|yЉ1|=|xЉ2|+|x+2Љ1|=|xЉ2|+|x+1|ЃЌШЛКѓгЩОјЖджЕгыЪ§жсЕФЙиЯЕПЩжЊЃЌ|xЉ2|+|x+1|БэЪОЪ§жсЩЯЪЕЪ§xЫљЖдгІЕФЕуЕНЪ§2КЭЉ1ЫљЖдгІЕФЕуЕФОрРыжЎКЭЃЌЦфзюаЁжЕЮЊ3.
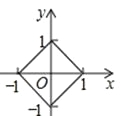
ЃЈ1ЃЉгЩЬтвтЃЌЕУ|x|+|y|=1.
ЫљгаЗћКЯЬѕМўЕФЕуPзщГЩЕФЭМаЮШчЭМЫљЪОЃК
ЃЈ2ЃЉЁпdЃЈMЃЌQЃЉ=|xЉ2|+|yЉ1|=|xЉ2|+|x+2Љ1|=|xЉ2|+|x+1|ЃЌ
гжЁпxПЩШЁвЛЧаЪЕЪ§ЃЌ|xЉ2|+|x+1|БэЪОЪ§жсЩЯЪЕЪ§xЫљЖдгІЕФЕуЕНЪ§2КЭЉ1ЫљЖдгІЕФЕуЕФОрРыжЎКЭЃЌЦфзюаЁжЕЮЊ3.
ЁрЕуMЃЈ2ЃЌ1ЃЉЕНжБЯпy=x+2ЕФжБНЧОрРыЮЊ3.