��Ŀ����
����Ŀ��![]() �ǵȱ������Σ���
�ǵȱ������Σ���![]() ������
������![]() �ϵ�һ�����㣨��
�ϵ�һ�����㣨��![]() �����
�����![]() �غϣ���
�غϣ���![]() ����
����![]() Ϊ�ߵĵȱ������Σ�����
Ϊ�ߵĵȱ������Σ�����![]() ��
��![]() ��ƽ���ߣ��ֱ�����
��ƽ���ߣ��ֱ�����![]() �ڵ�
�ڵ�![]() ������
������![]() ��
��
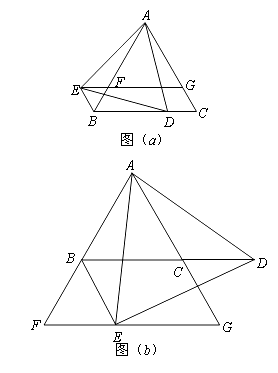
��1����ͼ��a����ʾ������![]() ���߶�
���߶�![]() ��ʱ��
��ʱ��
����֤��![]() ��
��
��̽�����ı���![]() ������������ı��Σ���˵�����ɣ�
������������ı��Σ���˵�����ɣ�
��2����ͼ��b����ʾ������![]() ��
��![]() ���ӳ�����ʱ��
���ӳ�����ʱ��
������1����������֤��̽�������������Ƿ���Ȼ��������ֱ��д��������˵�����ɣ�
������![]() �˶���ʲôλ��ʱ���ı���
�˶���ʲôλ��ʱ���ı���![]() �����Σ���˵�����ɣ�
�����Σ���˵�����ɣ�
���𰸡���1��������������ƽ���ı�����2������������BC��CD
���������⣺��1�� �� �� ��ABC����ADE���ǵȱ�������,
�� AE=AD,AB=AC,��EAD=��BAC=60��.
���� ��EAB=��EAD-��BAD,��DAC=��BAC-��BAD
�� ��EAB=��DAC,
�� ��AEB�ա�ADC�� ��������������������������������������������3�֣�
�� �ı���![]() ��ƽ���ı���. ��������������������������������6�֣�
��ƽ���ı���. ��������������������������������6�֣�
��2����1�������:
�� ��AEB�ա�ADC���� �ı���![]() ��ƽ���ı��Σ�������. ������������������8�֣�
��ƽ���ı��Σ�������. ������������������8�֣�
��3����BC��CDʱ���ı���BCFE�����Σ�������������������������������������9�֣�
���ɣ� ��������AEB�ա�ADC��
��BE��BC
���� BE��CD��
�� BC��CD��
�������ı���![]() ��ƽ���ı��Σ�
��ƽ���ı��Σ�
�� �ı���![]() �����Σ� ������������������������������������13�֣�
�����Σ� ������������������������������������13�֣�
��1����֤��������EAB����BAD����BAD����DAC��60�ȣ�������EAB����DAC����EA��DA��BA��CA������AEB�ա�ADC������������EBC����EBA����ABC����DCA����ABC��120�ȡ���ô��EBC����BCG��120�ȣ�60�ȣ�180�ȣ�����EB//GC����EG//BC����BCGEΪһƽ���ı��Ρ� ��2��BEGC��Ϊƽ���ı��Ρ��루1�����ƣ�����֤������ABEȫ���ڦ�ACD����ô��ABE����ACD��120�ȣ�������CBE����ACB��60�ȣ�����BE//GC����BC//EG���Ӷ���֤����3����ʹ���Ϊ���Σ�ֻ��BE��BC����BE��CD����ֻ��ѡȡD��ʹBC��CD���ɡ�

����Ŀ�������±��ش����⣺
x | 16 | 16.1 | 16.2 | 16.3 | 16.4 | 16.5 | 16.6 | 16.7 | 16.8 |
x2 | 256 | 259.21 | 262.44 | 265.69 | 268.96 | 272.25 | 175.56 | 278.89 | 282.24 |
��1��272.25��ƽ������������������
��2��![]() =��������������
=�������������� ![]() =��������������
=�������������� ![]() =������������
=������������
��3����![]() ����������Ϊa����4a����������
����������Ϊa����4a����������







