题目内容
【题目】渔夫在静水划船总是每小时5里,现在逆水行舟,水流速度是每小时3里;一阵风把他帽子吹落在水中,假如他没有发现,继续向前划行;等他发觉时人与帽子相距2.5里;

于是他立即原地调头追赶帽子,原地调转船头用了10分钟.
![]()
计算:
(1)求顺水速度,逆水速度是多少?
(2)从帽子丢失到发觉经过了多少时间?
(3)从发觉帽子丢失到捡回帽子经过了多少时间?
【答案】(1)顺水速度是每小时8里,逆水速度是每小时2里;(2)从帽子丢失到发觉经过了0.5小时;(3)从发觉帽子丢失到捡回帽子经过![]() 小时
小时
【解析】
(1)根据顺(逆)水速度、船在静水中的速度和水流的速度的关系即可求得;
(2) 根据逆水时船的速度以及水速表示出两者行驶的路程之和为2.5,列出一元一次方程即可求得;
(3)根据题意列出一元一次方程再考虑到原地掉头时间,即可求得.
(1)∵顺水速度=静水速度+水流速度,
逆水速度=静水速度﹣水流速度,
∴顺水速度是5+3=8,逆水速度是5﹣3=2,
答:顺水速度是每小时8里,逆水速度是每小时2里;
(2)设从帽子丢失到发觉经过了x小时.
根据题意,得:
![]() ,
,
解得:x=0.5,
答:从帽子丢失到发觉经过了0.5小时;
(3)设原地调转船头后到捡回帽子经过了y小时,
则从发觉帽子丢失到捡回帽子经过(y+![]() )小时.
)小时.
根据题意,得:
(5+3)y=2.5+3×(y+![]() )
)
解得:y=![]() .
.
∴y+![]() =
=![]()
答:从发觉帽子丢失到捡回帽子经过![]() 小时.
小时.

【题目】在春季运动会上,某学校教工组和学生组进行定点投篮比赛,每组均派五名选手参加,每名选手投篮十次,投中记1分,不中记零分,3分以上(含3分)视为合格,比赛成绩绘制成条形统计图如下:
投篮成绩条形统计图
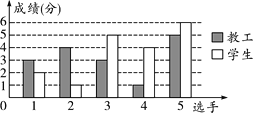
(1)请你根据条形统计图中的数据填写表格:
组别 | 平均数 | 中位数 | 方差 | 合格率 |
教工组 | ________ | 3 | ________ | 80% |
学生组 | 3.6 | ________ | 3.44 | 60% |
(2)如果小亮认为教工组的成绩优于学生组,你认为他的理由是什么?小明认为学生组成绩优于教工组,他的理由又是什么?
(3)若再让一名体育教师投篮后,六名教师成绩平均数大于学生组成绩的中位数,设这名体育教师命中m分,求m的值.