题目内容
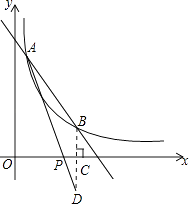
【题目】如图,一次函数y=﹣x+4的图象与反比例y= ![]() (k为常数,且k≠0)的图象交于A(1,a),B两点.
(k为常数,且k≠0)的图象交于A(1,a),B两点. 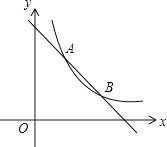
(1)求反比例函数的表达式及点B的坐标;
(2)在x轴上找一点P,使PA+PB的值最小,求PA+PB的最小值.
【答案】
(1)解:把点A(1,a)代入一次函数y=﹣x+4,
得a=﹣1+4,
解得a=3,
∴A(1,3),
点A(1,3)代入反比例函数y= ![]() ,
,
得k=3,
∴反比例函数的表达式y= ![]() ,
,
两个函数解析式联立列方程组得  ,
,
解得x1=1,x2=3,
∴点B坐标(3,1)
(2)解:作点B作关于x轴的对称点D,交x轴于点C,连接AD,交x轴于点P,此时PA+PB=PA+PD=AD的值最小,
∴D(3,﹣1),
∵A(1,3),
∴AD= ![]() =2
=2 ![]() ,
,
∴PA+PB的最小值为2 ![]() .
.
【解析】(1)把点A(1,a)代入一次函数y=﹣x+4,即可得出a,再把点A坐标代入反比例函数y= ![]() ,即可得出k,两个函数解析式联立求得点B坐标;(2)作点B作关于x轴的对称点D,连接AD,交x轴于点P,此时PA+PB=PA+PD=AD的值最小,然后根据勾股定理即可求得.
,即可得出k,两个函数解析式联立求得点B坐标;(2)作点B作关于x轴的对称点D,连接AD,交x轴于点P,此时PA+PB=PA+PD=AD的值最小,然后根据勾股定理即可求得.

练习册系列答案
 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目