题目内容
已知x1和x2是关于x的方程x2-2(m+1)x+m2+3=0的两实数根,
+
=22,则m的值是( )
| x | 2 1 |
| x | 2 2 |
分析:根据根与系数的关系得:x1+x2=2(m+1),x1•x2=m2+3,根据(x1+x2)2-2x1•x2=22得出4(m+1)2-2(m2+3)=22,求出m,再代入根的判别式进行检验即可.
解答:解:根据根与系数的关系得:x1+x2=2(m+1),x1•x2=m2+3,
∵
+
=22,
∴(x1+x2)2-2x1•x2=22,
4(m+1)2-2(m2+3)=22,
m1=-6,m2=2,
当m=-6时,方程为x2+10x+39=0,
△=102-4×1×39<0,方程无实数解,
即m=-6舍去;
当m=2时,方程为x2-6x+7=0,
△=(-6)2-4×1×7>0,方程有实数解,
故选B.
∵
| x | 2 1 |
| x | 2 2 |
∴(x1+x2)2-2x1•x2=22,
4(m+1)2-2(m2+3)=22,
m1=-6,m2=2,
当m=-6时,方程为x2+10x+39=0,
△=102-4×1×39<0,方程无实数解,
即m=-6舍去;
当m=2时,方程为x2-6x+7=0,
△=(-6)2-4×1×7>0,方程有实数解,
故选B.
点评:本题考查了根的判别式和根与系数的关系,注意:应用根与系数的关系得条件是b2-4ac≥0.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
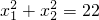 ,则m的值是
,则m的值是