题目内容
【题目】已知,四边形![]() 是平行四边形,
是平行四边形,![]() ,
,![]() 是
是![]() 上一点,满足
上一点,满足![]() 于点
于点![]() ,连接
,连接![]() .
.
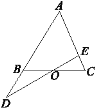
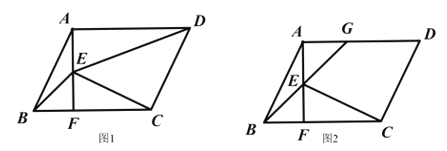
(1)如图![]() ,连接
,连接![]() ,若
,若![]() ,求
,求![]() 的周长;
的周长;
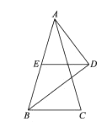
(2)如图![]() ,延长
,延长![]() ,交
,交![]() 于点
于点![]() ,若
,若![]() .求证:
.求证:![]() .
.
【答案】(1)![]() ;(2)证明见解析
;(2)证明见解析
【解析】
(1)因为四边形ABCD是平行四边形,可知AB=CD=![]() ,结合题目条件利用勾股定理即可得到
,结合题目条件利用勾股定理即可得到![]() ,
,![]() ,从而得到△ADE的周长;
,从而得到△ADE的周长;
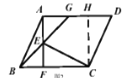
(2) 过点![]() 作
作![]() 于点
于点![]() ,根据题目条件可证的△CDH≌△ABF≌△EFC,根据全等三角形的性质,可得四边形AHCF是正方形,BF=EF=HD,证得△BEF是等腰直角三角形,从而得出结论.
,根据题目条件可证的△CDH≌△ABF≌△EFC,根据全等三角形的性质,可得四边形AHCF是正方形,BF=EF=HD,证得△BEF是等腰直角三角形,从而得出结论.
解:∵四边形ABCD是平行四边形,AB=![]()
∴AB=CD=![]()
∵![]() ,
,![]()
∴![]()
∴![]()
∵![]() ,
,![]()
∴![]()
又∵![]()
∴![]()
![]()
(2)过点![]() 作
作![]() 于点
于点![]() ,如图所示
,如图所示
∵四边形ABCD是平行四边形,AF⊥BC
∴CH=AF
在Rt△CHD和Rt△AFB中
![]()
![]() (HL)
(HL)
∴BF=HD
∵∠HCE+∠HCD=90°,∠HCE+ECF=90°
∴∠HCD= ECF
在△EFC和△HCD中
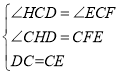
∴△EFC≌△HCD
∴△ABF≌△EFC
∴BF=EF=HD
∴HC=FC=AF=AH,∠FAH=90°
∴四边形AFCH是正方形
∴∠EBF=45°
∵AD∥BC
∴∠AGB=45°
∴AE=AG
∴EF=GH
∴DG=2HD

 备战中考寒假系列答案
备战中考寒假系列答案【题目】某校为了解七年级学生的体重情况,随机抽取了七年级m名学生进行调查,将抽取学生的体重情况绘制如下不完整的频数分布表和扇形统计图.
组别 | 体重(千克) | 人数 |
A | 37.5≤x<42.5 | 10 |
B | 42.5≤x<47.5 | n |
C | 47.5≤x<52.5 | 40 |
D | 52.5≤x<57.5 | 20 |
E | 57.5≤x<62.5 | 10 |

请根据图表信息回答下列问题:
(1)填空:①m=_____,②n=_____,③在扇形统计图中,C组所在扇形的圆心角的度数等于_______度;
(2)若把每组中各个体重值用这组数据的中间值代替(例如:A组数据中间值为40千克),则被调查学生的平均体重是多少千克?
(3)如果该校七年级有1000名学生,请估算七年级体重低于47.5千克的学生大约有多少人?