��Ŀ����
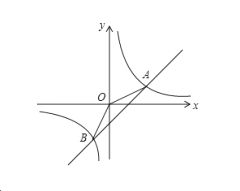
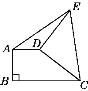
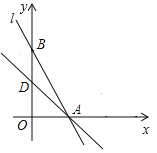
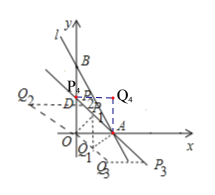
����Ŀ����֪��ͼ����ƽ��ֱ������ϵ�У�ֱ��AB�ֱ���x�ᡢy�ύ��A��B����(OA��OB)����OA��OB�ij��ֱ���һԪ���η���x2-18x+72=0����������DΪ�߶�OB���е㣬����D��AB�Ĵ������߶�AB�ཻ�ڵ�C��
(1)��A��B��������ꣻ
(2)�����C�ķ�������������ʽ��
(3)��֪��P��ֱ��AD�ϣ���ƽ�����Ƿ���ڵ�Q��ʹ��A��O��P��QΪ������ı���Ϊ���Σ������ڣ���ֱ��д����Q���ꣻ�������ڣ���˵�����ɣ�
���𰸡�(1) A(6��0)��B(0��12)�� (2) y=![]() �� (3) ��Q����Ϊ(3��-3)��(
�� (3) ��Q����Ϊ(3��-3)��(![]() ��
��![]() )��(
)��(![]() ��
��![]() )��(6��6)��
)��(6��6)��
��������
��1��ֱ�����һԪ���η��̵Ľ⣬���ɽ�����⣮
��2�������ֱ��AB��CD�Ľ���ʽ�����÷����������C���꣬���ɽ�����⣮
��3�����������ٵ�OA������AP1OQ1�ĶԽ���ʱ���ڵ�OAΪ����AP2Q2O�ı�ʱ���۵�OAΪ����AP3Q3O�ı�ʱ���ܵ�OAΪ����A Q4P4O�ı�ʱ����ʱ��P4���D�غϣ�����A Q4P4O��Ϊ�����Σ��ֱ���⼴�ɣ�
��1����x2-18x+72=0����ã�x=6��12��
��OA=6��OB=12��
��A(6��0)��B(0��12)��
��2����ֱ��AB�Ľ���ʽΪ��y=kx+b����A(6��0)��B(0��12)����ã�![]() �����
�����![]() ��
��
��ֱ��AB�Ľ���ʽΪ��y=-2x+12��
�ӳ�CD����x�����E��
��DC��AB��D(0��6)��
���AEC+��OAB=��OBA+��OAB=90�㣬
���AEC=��OBA��
�ߡ�DOE=��AOB��OD=OA=6��
��DOEAOB��AAS����
��OE=OB=12��
��E(-12��0)��
��ֱ��DC�Ľ���ʽΪ��y=kx+b��
��D(0��6)��E(-12��0)����y=kx+b���ã�![]() ����ã�
����ã�![]() ��
��
��ֱ��DC�Ľ���ʽΪ��y=![]() x+6��
x+6��
�� �����
�����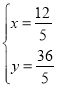 ��
��
�ཻ��C����(![]() ��
��![]() )��
)��
�����C�ķ����������Ľ���ʽΪ��y=![]() ��
��
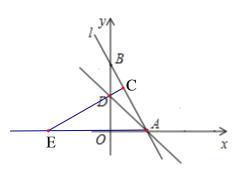
��3���ٵ�OA������AP1OQ1�ĶԽ���ʱ����֪P1(3��3)��
��P1��Q1����x��Գƣ�
��Q1(3��-3)��
�ڵ�OAΪ����AP2Q2O�ı�ʱ��
��OA=AP2=P2Q2=6����OAD=45�㣬
��P2(6-3![]() ��3
��3![]() )��Q2(-3
)��Q2(-3![]() ��3
��3![]() )��
)��
�۵�OAΪ����AP3Q3O�ı�ʱ��ͬ���ɵ�Q3(3![]() ��-3
��-3![]() )��
)��
�ܵ�OAΪ����A Q4P4O�ı�ʱ����ʱ��P4���D�غϣ�����A Q4P4O��Ϊ�����Σ�Q4(6��6)��
�������������������ĵ�Q����Ϊ(3��-3)��(![]() ��
��![]() )��(
)��(![]() ��
��![]() )��(6��6)��
)��(6��6)��

 �߽�������ϵ�д�
�߽�������ϵ�д�