题目内容
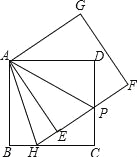
【题目】如图,在边长为6的正方形ABCD中,将正方形ABCD绕点A逆时针旋转角度α(0°<α<90°),得到正方形AEFG,EF交线段CD于点P,FE的延长线交线段BC于点H,连接AH、AP.
(1)求证:△ADP≌△AEP;
(2)①求∠HAP的度数;②判断线段HP、BH、DP的数量关系,并说明理由;
(3)连接DE、EC、CF、DF得到四边形CFDE,在旋转过程中,四边形CFDE能否为矩形?若能,求出BH的值;若不能,请说明理由.
【答案】(1)证明详见解析;(2)①45°;②HP=HE+EP=HB+DP;(3)能,2.
【解析】
试题分析:(1)根据旋转变换的性质得到AB=AE,∠AEP=∠ABH=90°,根据正方形的性质得到AD=AB,∠D=90°,根据直角三角形的全等的判定定理证明即可;
(2)证明Rt△COH≌Rt△CDH,得到∠OCH=∠DCH,HO=DH,等量代换即可;
(3)根据矩形的判定定理证明四边形AEBD是矩形,设点H的坐标为(x,0),根据勾股定理列出方程,解方程求出x的值,得到点H的坐标.
试题解析:(1)∵将正方形ABCD绕点A逆时针旋转角度α,
∴AB=AE,∠AEP=∠ABH=90°,
∵四边形ABCD是正方形,
∴AB=AD,∠D=90°,
∴AE=AD,∠D=∠AEP=90°
在Rt△ADP与Rt△AEP中,
AD=AE,AP=AP,
∴Rt△ADP≌Rt△AEP;
(2)∵∠AEP=90°,
∴∠AEH=90°,
在Rt△ABH与Rt△AEH中,
AB=AE,AH=AH,
∴Rt△ABH≌Rt△AEH,
∴∠BAH=∠EAH,BO=HE,
∵Rt△AEP≌Rt△ADP,
∴∠EAP=∠DAP,EP=DP,
∴∠HAP=∠HAE+∠EAP=![]() ∠BAD=45°,
∠BAD=45°,
HP=HE+EP=HB+DP;
(3)当P是CD中点时,四边形CFDE是矩形,
∵P是CD中点,
∴DP=CP=![]() CD,
CD,
由(2)得EP=DP,
又∵CD=EF,
∴DG=![]() DE,
DE,
∴DP=PC=PE=PF,
∴四边形CFDE是矩形,
设BH=x,
则HE=BH=x,PE=PD=PC=3,CH=6﹣x,
由勾股定理得,![]() ,
,
解得,x=2,即BH=2.