题目内容
【题目】已知，如图，∠B=∠C=90 ，M是BC的中点，DM平分∠ADC.
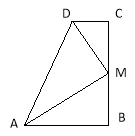
（1）若连接AM，则AM是否平分∠BAD？请你证明你的结论；
（2）线段DM与AM有怎样的位置关系？请说明理由.
【答案】（1）平分；（2）DM⊥AM
【解析】
试题分析：（1）过点M作ME⊥AD于点E，再根据角平分线的性质得到MC=ME，由M为BC的中点可得MC=MB即得ME=MB，再结合MB⊥AB，ME⊥AD即可证得结论；
（2）根据角平分线的性质可得∠ADM=
∠ADC，∠DAM=
∠BAD，由∠B=∠C=90可得AB//CD，即可得到∠ADC+∠BAD=180，再根据角平分线的性质求解即可.
（1）AM是平分∠BAD，
理由如下：过点M作ME⊥AD于点E
∵DM平分∠ADC且MC⊥ CD，ME⊥AD
∴MC=ME
∵M为BC的中点
∴MC=MB
∴ME=MB
∵MB⊥AB，ME⊥AD
∴AM平分∠BAD；
（2）DM⊥AM
理由如下：∵DM平分∠ADC
∴∠ADM=∠ADC
∵AM平分∠BAD
∴∠DAM=∠BAD
∵∠B=∠C=90
∴AB//CD
∴∠ADC+∠BAD=180
∴∠ADM+∠DAM=∠ADC+∠BAD=（∠ADC+∠BAD）=90
∴∠DMA=90
∴DM⊥AM.
练习册系列答案
相关题目
