题目内容
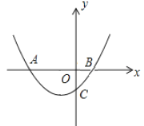
【题目】如图,已知抛物线![]() 交x轴于A(-4,0),B两点,交y轴于点C(0,-2).
交x轴于A(-4,0),B两点,交y轴于点C(0,-2).
(1)求抛物线的解析式;
(2)过点M(m,0)(-4<m<0)且垂直于x轴的直线与抛物线![]() 相交于点N,求线段OM+MN的最大值.
相交于点N,求线段OM+MN的最大值.
【答案】(1)y=![]() x2+
x2+![]() -2;(2)OM+MN的最大值为
-2;(2)OM+MN的最大值为![]() .
.
【解析】
(1)把点A,C的坐标分别代入y=ax2+![]() +c即可求出a、c的值,即可得出抛物线解析式;
+c即可求出a、c的值,即可得出抛物线解析式;
(2)设点M(m,0),则N(m,![]() ),表达出OM+MN=-m
),表达出OM+MN=-m![]() 转化为函数最大值问题进行解答即可;
转化为函数最大值问题进行解答即可;
(1)把点A,C的坐标分别代入y=ax2+![]() +c,
+c,
得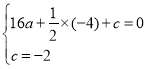
解得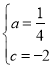 ,∴抛物线的解析式为y=
,∴抛物线的解析式为y=![]() x2+
x2+![]() -2,
-2,
(2)∵点M(m,0),直线MN⊥x轴,且点N在抛物线上,
∴N(m,![]() ).
).
又∵-4<m<0,
∴OM=-m,MN= 0-(![]() )=
)=![]() ,
,
∴OM+MN=-m+![]() =
=![]()
∵![]() <0,
<0,
∴当m=-3时,OM+MN取得最大值,最大值为![]()

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案
相关题目
【题目】电影《我和我的祖国》上映以来好评如潮,某影评平台随机调查了部分观众对这部电影的评分(满分10分),并将调查结果制成了如下不完整的统计图表(表中每组数据不包括最小值,包括最大值):
等级 | 频数 | 频率 |
A等(9.6分~10分) | a | 0.7 |
B等(8.8分~9.6分) | 3 | 0.15 |
C等(8.2分~8.8分) | b | c |
D等(8.2分及以下) | 1 | 0.05 |
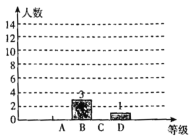
请根据图表信息,解答下列问题:
(1)这次共随机调查了_______名观众,a=______;b=______;c=______;
(2)补全条形统计图;
(3)若某电影院同时上映《我和我的祖国》、《中国机长》和《烈火英雄》,红红和兰兰分别选择其中一部电影观看,求她们选中同一部电影的概率.