题目内容
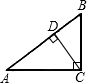如图，Rt△ABC中，∠ACB=90°，CD⊥AB于点D，BC=3，AC=4，设∠BCD=α，则tanα的值为（ ）A、
| ||
B、
| ||
C、
| ||
D、
|
分析：证明∠BCD=∠A=α，在Rt△ABC中求tanα的值．
解答：解：∵∠ACB=90°，CD⊥AB，
∴∠BCD+∠B=90°，∠A+∠B=90°，
∴∠BCD=∠A=α．
∴tanα=tanA=
=
．
故选A．
∴∠BCD+∠B=90°，∠A+∠B=90°，
∴∠BCD=∠A=α．
∴tanα=tanA=
| BC |
| AC |
| 3 |
| 4 |
故选A．
点评：考查灵活进行等量转换的能力．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
如图，Rt△ABC中，∠ACB=90°，tanB=
如图，Rt△ABC中，∠C=90°，BC=3，AC=4，若△ABC∽△BDC，则CD=（ ）
如图，Rt△ABC中，∠C=90°，△ABC的内切圆⊙0与BC、CA、AB分别切于点D、E、F．
如图，Rt△ABC中，∠ABC=90゜，BD⊥AC于D，∠CBD=α，AB=3，BC=4．