题目内容
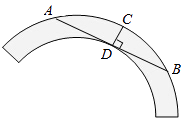
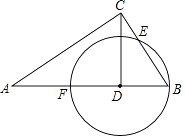
【题目】如图,半径为6cm的⊙O中,C、D为直径AB的三等分点,点E、F分别在AB两侧的半圆上,∠BCE=∠BDF=60°,连接AE、BF,则图中两个阴影部分的面积为cm2 . 
【答案】6 ![]()
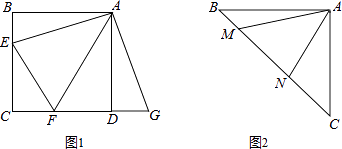
【解析】解:如图作△DBF的轴对称图形△CAG,作AM⊥CG,ON⊥CE, 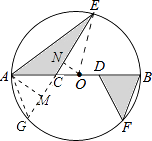
∵△DBF的轴对称图形△CAG,
由于C、D为直径AB的三等分点,
∴△ACG≌△BDF,
∴∠ACG=∠BDF=60°,
∵∠ECB=60°,
∴G、C、E三点共线,
∵AM⊥CG,ON⊥CE,
∴AM∥ON,
∴ ![]() ,
,
在Rt△ONC中,∠OCN=60°,
∴ON=sin∠OCNOC= ![]() OC,
OC,
∵OC= ![]() OA=2,
OA=2,
∴ON= ![]() ×2=
×2= ![]() ,
,
∴AM=2 ![]() ,
,
∵ON⊥GE,
∴NE=GN= ![]() GE,
GE,
连接OE,
在Rt△ONE中,NE= ![]() =
= ![]() =
= ![]() ,
,
∴GE=2NE=2 ![]() ,
,
∴S△AGE= ![]() GEAM=
GEAM= ![]() ×2
×2 ![]() ×2
×2 ![]() =6
=6 ![]() ,
,
∴图中两个阴影部分的面积为6 ![]() ,
,
所以答案是:6 ![]() .
.
【考点精析】本题主要考查了含30度角的直角三角形和勾股定理的概念的相关知识点,需要掌握在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半;直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2才能正确解答此题.

 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案【题目】为了保护环境,某开发区综合治理指挥部决定购买A,B两种型号的污水处理设备共10台.已知用90万元购买A型号的污水处理设备的台数与用75万元购买B型号的污水处理设备的台数相同,每台设备价格及月处理污水量如下表所示:
污水处理设备 | A型 | B型 |
价格(万元/台) | m | m﹣3 |
月处理污水量(吨/台) | 220 | 180 |
(1)求m的值;
(2)由于受资金限制,指挥部用于购买污水处理设备的资金不超过165万元,问有多少种购买方案?并求出每月最多处理污水量的吨数.