题目内容
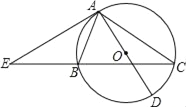
【题目】己知:如图①,直线MN⊥直线PQ,垂足为O,点A在射线OP上,点B在射线OQ上(A、B不与O点重合),点C在射线ON上,过点C作直线![]() ,点D在点C的左边。
,点D在点C的左边。
(1)若BD平分∠ABC,![]() ,则
,则![]() _____°;
_____°;
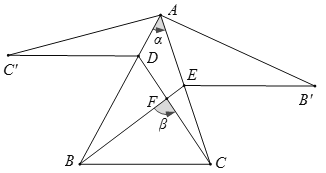
(2)如图②,若![]() ,作∠CBA的平分线交OC于E,交AC于F,试说明
,作∠CBA的平分线交OC于E,交AC于F,试说明![]() ;
;
(3)如图③,若∠ADC=∠DAC,点B在射线OQ上运动,∠ACB的平分线交DA的延长线于点H.在点B运动过程中![]() 的值是否变化?若不变,求出其值;若变化,求出变化范围.
的值是否变化?若不变,求出其值;若变化,求出变化范围.

【答案】(1)10;(2)证明见解析;(3)不变,![]()
【解析】
(1)根据两直线平行,内错角相等得∠ABD=![]() ,由BD平分∠ABC得∠ABC=2∠ABD=80°,根据垂直即可得∠OCB的度数;
,由BD平分∠ABC得∠ABC=2∠ABD=80°,根据垂直即可得∠OCB的度数;
(2)利用∠CFE+∠CBF=90°,∠OBE+∠OEB=90°,求出∠CEF=∠CFE;
(3)由∠ABC+∠ACB=2∠DAC,∠H+∠HCA=∠DAC,∠ACB=2∠HCA,求出∠ABC=2∠H,即可得答案.
解:(1)∵直线![]() ,
,![]() ,
,
∴∠ABD=![]() ,
,
∵BD平分∠ABC,
∴∠ABC=2∠ABD=80°,
又∵直线MN⊥直线PQ,
∴∠OCB=90°-∠ABC=10°;
(2)∵![]() ,∴
,∴![]()
∴![]()
∵直线![]() 直线PQ
直线PQ
∴![]()
∵![]()
∴![]()
∵BF是∠CBA的平分线,
∴![]()
∴![]() ;
;
(3)不变
∵直线![]() ,
,
∴![]()
∵![]() ,
,
∴![]()
∵![]()
∴![]()
∵![]()
span>∴![]()
∵CH是∠ACB的平分线
∴![]()
∴![]()
∴![]() .
.
故答案为:(1)10;(2)证明见解析;(3)不变,![]() .
.

【题目】小亮想了解一根弹簧的长度是如何随所挂物体质量的变化而变化的,他把这根弹簧的上端固定,在其下端悬挂物体.下面是小亮测得的弹簧的长度y与所挂物体质量x的几组对应值.
所挂质量x/kg | 0 | 1 | 2 | 3 | 4 | 5 |
弹簧长度y/cm | 30 | 32 | 34 | 36 | 38 | 40 |
(1)上表所反映的变化过程中的两个变量,________是自变量,________是因变量;
(2)直接写y与x的关系式;
(3)当弹簧长度为130cm(在弹簧承受范围内)时,求所挂重物的质量.