题目内容
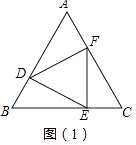
【题目】如图,过∠AOB平分线上一点C作CD∥OB交OA于点D,E是线段OC的中点,请过点E画直线分别交射线CD、OB于点M、N,探究线段OD、ON、DM之间的数量关系,并证明你的结论. 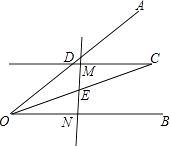
【答案】解:①当点M在线段CD上时,线段OD、ON、DM之间的数量关系是:OD=DM+ON. 证明:如图1,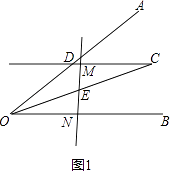 ,
,
∵OC是∠AOB的平分线,
∴∠DOC=∠C0B,
又∵CD∥OB,
∴∠DCO=∠C0B,
∴∠DOC=∠DC0,
∴OD=CD=DM+CM,
∵E是线段OC的中点,
∴CE=OE,
∵CD∥OB,
∴ ![]() ,
,
∴CM=ON,
又∵OD=DM+CM,
∴OD=DM+ON.
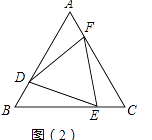
②当点M在线段CD延长线上时,线段OD、ON、DM之间的数量关系是:OD=ON﹣DM.
证明:如图2,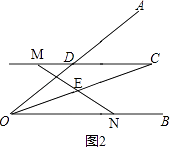 ,
,
由①,可得
OD=DC=CM﹣DM,
又∵CM=ON,
∴OD=DC=CM﹣DM=ON﹣DM,
即OD=ON﹣DM.
【解析】①当点M在线段CD上时,线段OD、ON、DM之间的数量关系是:OD=DM+ON.首先根据OC是∠AOB的平分线,CD∥OB,判断出∠DOC=∠DC0,所以OD=CD=DM+CM;然后根据E是线段OC的中点,CD∥OB,推得CM=ON,即可判断出OD=DM+ON,据此解答即可.②当点M在线段CD延长线上时,线段OD、ON、DM之间的数量关系是:OD=ON﹣DM.由①,可得OD=DC=CM﹣DM,再根据CM=ON,推得OD=ON﹣DM即可.

练习册系列答案
相关题目