Question

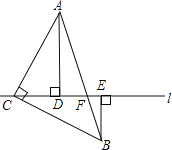
【题目】如图,将等腰直角三角形ABC的直角顶点置于直线上,且过A，B两点分别作直线l的垂线,垂足分别为D，E.

（1）请你在图中找出一对全等三角形,并写出证明过程;

（2）若BE=3，DE=5，求AD的长.

Answer 1

【答案】（1）全等三角形为: ≌.证明见解析；（2）AD=8.

【解析】

（1）观察图形，结合已知条件，可知全等三角形为：△ACD≌△CBE．根据AAS即可证明；
（2）由（1）知△ACD≌△CBE，根据全等三角形的对应边相等，得出CD=BE=3，AD=CE，所以CE=3+5=8，即可得AD的长．

（1）全等三角形为: ≌.

证明:由题意知,,

∴,

在与中,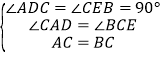

∴ .

(2)由1知, ,

∴,,

∴.

故答案为：（1）全等三角形为: △ACD≌△CBE.证明见解析；（2）AD=8.