题目内容
【题目】已知OA⊥OB,OC⊥OD.
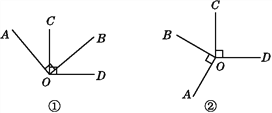
(1)如图①,若∠BOC=50°,求∠AOD的度数.
(2)如图②,若∠BOC=60°,求∠AOD的度数.
(3)根据(1)(2)结果猜想∠AOD与∠BOC有怎样的关系?并根据图①说明理由.
(4)如图②,若∠BOC∶∠AOD=7∶29,求∠COB和∠AOD的度数.
【答案】(1)130°;(2)120°;(3)互补;(4)∠COB=35°,∠AOD=145°.
【解析】试题分析:(1)根据垂线的定义,可得∠AOB与∠COD的度数,根据余角的定义,可得∠AOC,根据角的和差,可得答案;
(2)根据角的和差,可得答案;
(3)根据角的和差,可得答案;
(4)根据按比例分配,可得答案.
试题解析: (1)由OA⊥OB,OC⊥OD,
得∠AOB=∠COD=90°,
由余角的定义,得∠AOC=∠AOB∠BOC=90°50°=40°,
由角的和差,得∠AOD=∠AOC+∠COD=40°+90°=130°;
(2)由OA⊥OB,OC⊥OD,得∠AOB=∠COD=90°,
由角的和差,得∠AOD=360°∠AOB∠BOC∠COD=360°90°60°90°=120°,
(3)∠AOD+∠BOC=180,
∠AOD+∠BOC=130°+50°=180°;
(4)由角的和差,得∠AOD+∠BOC=360°∠AOB∠COD=180°,
按比例分配,得∠BOC=180°×![]() =35°
=35°
∠AOD=180°×![]() =145°.
=145°.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目



