题目内容
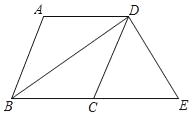
【题目】在美化校园的活动中,某兴趣小组想借助如图所示的直角墙角(两边足够长),用28m长的篱笆围成一个矩形花园ABCD(篱笆只围AB,BC两边),设AB=xm,花园的面积为Sm2.
(1)若花园的面积为192m2,求x的值;
(2)写出花园面积S与x的函数关系式.x为何值时,花园面积S有最大值?最大值为多少?
(3)若在P处有一棵树与墙CD,AD的距离分别是a(14≤a≤22)和6m,要将这棵树围在花园内(含边界,不考虑树的粗细),设花园面积S的最大值为y,直接写出y与a的关系式.

【答案】(1)花园的面积为192m2,x的值为12m或16m;(2)x为14m时,花园面积S有最大值,最大值为196m2;(3)当x=28﹣a时,函数有最大值,y=﹣(14﹣a)2+196.
【解析】
(1)根据题意得出长×宽=192,进而得出答案;
(2)由题意可得出:S=x(28x)=x2+28x=(x14)2+196,再利用二次函数的性质求解;
(3)根据题意确定x的取值范围,利用二次函数增减性计算即可.
解:(1)依题意得 S=x(28﹣x),
当S=192时,有S=x(28﹣x)=192,
即x2﹣28x+192=0,
解得:x1=12,x2=16,
答:花园的面积为192m2,x的值为12m或16m;
(2)由题意可得出:
S=x(28﹣x)
=﹣x2+28x
=﹣(x﹣14)2+196,
答:x为14m时,花园面积S有最大值,最大值为196m2;
(3)依题意得:
![]() ,
,
解得:6≤x≤28﹣a,
S=x(28﹣x)=﹣x2+28x=﹣(x﹣14)2+196,
∵a=﹣1<0,当x≤14,y随x的增大而增大,
又6≤x≤28﹣a,
∴当x=28﹣a时,函数有最大值,
∴y=﹣(28﹣a﹣14)2+196=﹣(14﹣a)2+196.

【题目】某班开展安全知识竞赛活动,班长将所有同学的成绩(得分为整数,满分为100分)分成四类,并制作了如下的统计图表:
类别 | 成绩 | 频数 |
甲 | 60≤m<70 | 5 |
乙 | 70≤m<80 | a |
丙 | 80≤m<90 | 10 |
丁 | 90≤m≤100 | 5 |

根据图表信息,回答下列问题:
(1)该班共有学生________人;表中a=________;
(2)将丁类的五名学生分别记为A、B、C、D、E,现从中随机挑选两名学生参加学校的决赛,请借助树状图、列表或其他方式求B一定能参加决赛的概率.