��Ŀ����
����Ŀ��ij��ѧС������ѧ�����У��о������κ������ε�����ʱ����������̽����
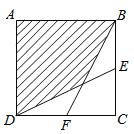
�ڡ�ABC�У���BAC��90�㣬AB��AC����DΪֱ��BC��һ����(��D����B��C�غ�)��
��ADΪ����AD�Ҳ���������ADEF������CF��
(1).��ͼ1������D���߶�BC��ʱ��
��.BC��CF��λ�ù�ϵΪ��________________________________��
��.BC��CD��CF֮���������ϵΪ��_______________________________.
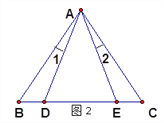
(2).��ͼ2������D���߶�CB���ӳ�����ʱ�����ۢ٣����Ƿ���Ȼ��������������
�����֤������������������д����ȷ�����ٸ���֤����
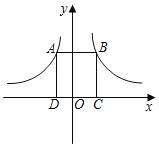
(3).��ͼ3����ͼ2�е� AB��AC�ı��AB��kAC��������ADEF�ijɾ���ADEF����AD=kAF,������������ �������߶�BD��CF֮��Ĺ�ϵ��˵������.


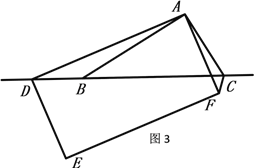
���𰸡�(1) ��BC��CF��λ�ù�ϵΪ��BC��CF ����BC��CD��CF֮���������ϵΪ��BC=CF+CD��֤����������(2)���ۢٳ������ڲ�������BC��CD��CF֮���������ϵΪBC=CD-CF��CD=BC+CF��֤����������(3).������ϵBD=kCF��λ�ù�ϵBC��CF��֤��������.
��������
��1�����������α���ȣ����������Σ�֤��![]() ABD ��
ABD �� ![]() AFCȫ�ȣ���֤����FCB=90����
AFCȫ�ȣ���֤����FCB=90����
��2�����ⷽ���ο���1����
��3���ο���1����ԭ����֤��![]() ABD ��
ABD �� ![]() AFC���ƣ�����֤��BD=kCF��
AFC���ƣ�����֤��BD=kCF��
�⣺��1��![]() AB��AC��AD=AF,
AB��AC��AD=AF,
![]() ��BAD+��DAC=��FAC+��DAC,
��BAD+��DAC=��FAC+��DAC,
![]() ��BAD=��CAF,
��BAD=��CAF,
![]() ABD
ABD![]()
![]() AFC��
AFC��
![]() ��ABD=��ACF.
��ABD=��ACF.
![]() .
.
![]() BC��CF
BC��CF
![]() C=BC+CF.
C=BC+CF.
��2��![]() AB��AC��AD=AF,
AB��AC��AD=AF,
![]() ��BAD+��DAC=��FAC+��DAC,
��BAD+��DAC=��FAC+��DAC,
![]() ��BAD=��CAF,
��BAD=��CAF,
![]() ABD
ABD![]()
![]() AFC��
AFC��
![]() ��ADB=��AFC.
��ADB=��AFC.
![]() . BC��CF
. BC��CF
���ۢٳ������ڲ�������
![]() CD=BC+CF.
CD=BC+CF.
��3��![]() AB��kAC��AD=kAF,
AB��kAC��AD=kAF,
![]() ��BAD+��DAC=��FAC+��DAC,
��BAD+��DAC=��FAC+��DAC,
![]() ��BAD=��CAF,
��BAD=��CAF,
![]() ABD
ABD![]()
![]() AFC��
AFC��
![]() BD=kCF.
BD=kCF.
![]() ��ADB=��AFC.
��ADB=��AFC.
![]() .
.
BC��CF.

����Ŀ��С��ͬѧ�Ӽҵ�ѧУ��![]() ��
��![]() ������ͬ�Ĺ�����·��Ϊ�˽���߷��ڼ���������·�ϵĹ������Ӽص��ҵص���ʱ�������ÿ����·�����ѡȡ��500����εĹ��������ռ�����Щ��εĹ�������ʱ����λ�����ӣ������ݣ�ͳ�����£�
������ͬ�Ĺ�����·��Ϊ�˽���߷��ڼ���������·�ϵĹ������Ӽص��ҵص���ʱ�������ÿ����·�����ѡȡ��500����εĹ��������ռ�����Щ��εĹ�������ʱ����λ�����ӣ������ݣ�ͳ�����£�
��������ʱ Ƶ�� ������·�� |
|
|
|
| �ܼ� |
| 59 | 151 | 166 | 124 | 500 |
| 43 | 57 | 149 | 251 | 500 |
�ݴ˹��ƣ���߷��ڼ䣬����![]() ��·����ʱ������35�������ĸ���Ϊ__________����Ҫ��40����֮�ڵ���ѧУ��Ӧ����ѡ�����__________����
��·����ʱ������35�������ĸ���Ϊ__________����Ҫ��40����֮�ڵ���ѧУ��Ӧ����ѡ�����__________����![]() ��
��![]() ����·��
����·��
����Ŀ���Ķ��������ݣ�����Ҫ�������⣺
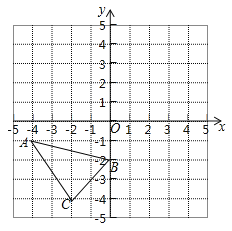
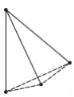
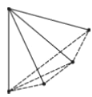
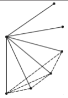
���⣺����ƽ���ڣ���֪�ֱ���2���㣬3���㣬4���㣬5���㣬����![]() ���㣬�������������㶼����ͬһ��ֱ���Ͼ���ÿ���㻭һ��ֱ�ߣ����ǿ��Էֱ�����ֱ�ߣ���
���㣬�������������㶼����ͬһ��ֱ���Ͼ���ÿ���㻭һ��ֱ�ߣ����ǿ��Էֱ�����ֱ�ߣ���
̽����Ϊ�˽��������⣬ϣ��С���ͬѧ�ǣ���������±������̽������Ϊ�˷����о����⣬ͼ��ÿ���߶α�ʾ���߶����˵��һ��ֱ�ߣ�
���� | 2 | 3 | 4 | 5 | �� |
|
ʾ��ͼ |
|
|
|
| �� |
|
ֱ������ | 1 |
|
|
| �� |
�����������⣺
��1�������ϣ��С����ɣ���ֱ��д�����ۣ���ƽ����������ʱ��ֱ������Ϊ______��
��2����ijͬѧ���ձ����еķ�����������28��ֱ�ߣ����ƽ�����ж��ٸ���֪�㣿