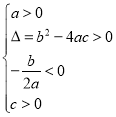题目内容
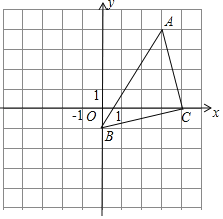
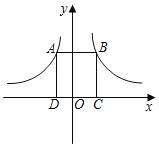
【题目】如图，反比例函数y＝
与y＝
的图象上分别有一点A，B，且AB∥x轴，AD⊥x轴于D，BC⊥x轴于C，若矩形ABCD的面积为8，则b﹣a＝（ ）
A.8B.﹣8C.4D.﹣4
【答案】A
【解析】
根据反比例函数系数k的几何意义得到|a|＝S矩形ADOE，|b|＝S矩形BCOE，进而得到|b|+|a|＝8，然后根据a＜0，b＞0可得答案．
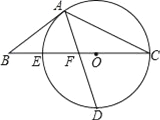
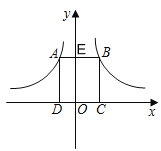
解：如图，∵AB∥x轴，AD⊥x轴于D，BC⊥x轴于C，
∴|a|＝S矩形ADOE，|b|＝S矩形BCOE，
∵矩形ABCD的面积为8，
∴S矩形ABCD＝S矩形ADOE+S矩形BCOE＝8，
∴|b|+|a|＝8，
∵反比例函数y＝
在第二象限，反比例函数y＝
在第一象限，
∴a＜0，b＞0，
∴|b|+|a|＝b﹣a＝8，
故选：A．
练习册系列答案
相关题目
【题目】阅读下列材料：有这样一个问题：关于
的一元二次方程
有两个不相等的且非零的实数根探究
，
，
满足的条件.
小明根据学习函数的经验，认为可以从二次函数的角度看一元二次方程，下面是小明的探究过程：①设一元二次方程对应的二次函数为
；
②借助二次函数图象，可以得到相应的一元二次中，，满足的条件，列表如下：
方程根的几何意义：
方程两根的情况 | 对应的二次函数的大致图象 |
|
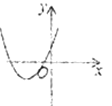
方程有两个不相等的负实根 |
|
|
____________ |
|
|
方程有两个不相等的正实根 | ____________ | ____________ |
（1）参考小明的做法，把上述表格补充完整；
（2）若一元二次方程
有一个负实根，一个正实根，且负实根大于-1，求实数
的取值范围.
