题目内容
【题目】将一副三角板![]() 与
与![]() (其中
(其中![]() ,
,![]() ,
,![]() )如图摆放,
)如图摆放,![]() 中
中![]() 所对的直角边与
所对的直角边与![]() 的斜边恰好重合。以
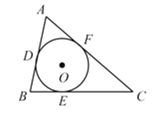
的斜边恰好重合。以![]() 为直径的圆经过点C,且与
为直径的圆经过点C,且与![]() 相交于点E,连接
相交于点E,连接![]() ,连接
,连接![]() 并延长交
并延长交![]() 于F.
于F.
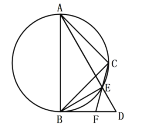
(1)求证:![]() 平分
平分![]() ;
;
(2)求![]() 与
与![]() 的面积的比值.
的面积的比值.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)根据同弧所对的圆周角相等可得![]() ,
,![]() ,根据三角形的外角性质可得
,根据三角形的外角性质可得![]() ,由直径所对的圆周角为90°得∠BED=∠AEB=90°,所以可得
,由直径所对的圆周角为90°得∠BED=∠AEB=90°,所以可得![]() ,结论可证;
,结论可证;
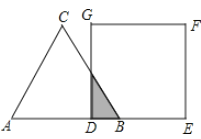
(2)过F作FG⊥BE,FH⊥AD,分别于BE、AD相交于G、H,根据角平分线的性质可得FG=FH,表示![]() 与
与![]() 的面积的比值,借助正切可求得它们的比值为
的面积的比值,借助正切可求得它们的比值为![]() .
.
(1)∵AB为![]() 的直径,
的直径,
∴∠BED=∠AEB=90°,
∵![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
![]() ,
,
∴![]()
![]()
∴![]() ,即
,即![]() 平分
平分![]() .
.
(2)如图,过F作FG⊥BE,FH⊥AD,分别于BE、AD相交于G、H.
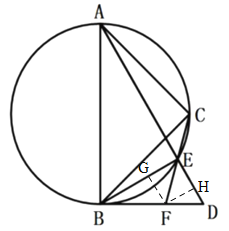
∵∠BED=90°,∠D=60°,
∴在Rt△BDE中,![]() ,
,
∵FG⊥BE, FH⊥AD,![]() 平分
平分![]() ,
,
∴FG=FH,
∴![]() ,故
,故![]() 与
与![]() 的面积的比值为
的面积的比值为![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
【题目】在一个不透明的口袋里装有只有颜色不同的黑、白两种颜色的球共5只.某学习小组做摸球实验,将球搅匀后从中随机摸出一个球记下颜色,再把它放回袋中,不断重复.下表是活动进行中的一组统计数据:
摸球的次数 n | 100 | 150 | 200 | 500 | 800 | 1000 |
摸到白球的次数 m | 58 | 96 | 116 | 295 | 484 | 601 |
摸到白球的频率 | 0.58 | 0.64 | 0.58 | 0.59 | 0.605 | 0.601 |
(1)请估计:当n很大时,摸到白球的频率将会接近 (结果精确到0.1);
(2)试估算口袋中黑球有 只,白球有 只;
(3)在(2)的结论下,请你用列表或树状图求出随机摸出两个球都是白球的概率.