题目内容
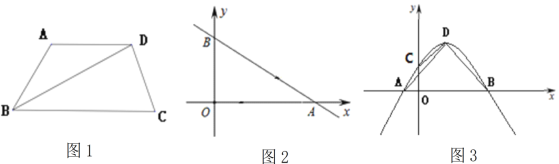
【题目】（2017宁夏）在边长为2的等边三角形ABC中，P是BC边上任意一点，过点 P分别作 PM⊥A B，PN⊥AC，M、N分别为垂足．
（1）求证：不论点P在BC边的何处时都有PM+PN的长恰好等于三角形ABC一边上的高；
（2）当BP的长为何值时，四边形AMPN的面积最大，并求出最大值．
【答案】【（1）证明见解析；（2）当BP=1时，四边形AMPN的面积最大，最大值是
．
【解析】
试题（1）连接AP，过C作CD⊥AB于D，根据等边三角形的性质得到AB=AC，根据三角形的面积公式列方程即可得到结论；
（2）设BP=x，则CP=2﹣x，由△ABC是等边三角形，得到∠B=∠C=60°，解直角三角形得到BM=
x，PM=
x，CN=（2﹣x），PN=（2﹣x），根据二次函数的性质即可得到结论．
试题解析：（1）连接AP，过C作CD⊥AB于D，
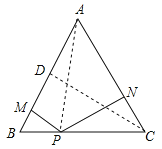
∵△ABC是等边三角形，∴AB=AC，∵S△ABC=S△ABP+S△ACP，∴ ABCD=ABPM+ACPN，∴PM+PN=CD，即不论点P在BC边的何处时都有PM+PN的长恰好等于三角形ABC一边上的高；
（2）设BP=x，则CP=2﹣x，∵△ABC是等边三角形，∴∠B=∠C=60°，∵PM⊥AB，PN⊥AC，∴BM=x，PM=x，CN=（2﹣x），PN=（2﹣x），∴四边形AMPN的面积=×（2﹣x）x+×[2﹣（2﹣x）] 
（2﹣x）=
=
，∴当BP=1时，四边形AMPN的面积最大，最大值是
．
【题目】在一个不透明的口袋里装有只有颜色不同的黑、白两种颜色的球共10只，某学习小组做摸球实验，将球搅匀后从中随机摸出一个球记下颜色，再把它放回袋中，不断重复．下表是活动进行中的一组统计数据：
摸球的次数 | 100 | 150 | 200 | 500 | 800 | 1000 |
摸到白球的次数 | 58 | 96 | 116 | 295 | 484 | 601 |
摸到白球的频率 | 0.58 | 0.64 | 0.58 | 0.59 | 0.605 | 0.601 |
（1）请估计：当
很大时，摸到白球的频率将会接近 ；（保留二个有效数字）
（2）试估算口袋中黑、白两种颜色的球各有多少只？
（3）请画树状图或列表计算：从中一次摸两只球，这两只球颜色不同的概率是多少？
