题目内容
如图抛物线y=a(x-1)2+4与x轴交于A、B两点,与y轴交于点C,D是抛物线的顶点,已知CD=| 2 |
(1)求抛物线的解析式;
(2)在抛物线上共有三个点到直线BC的距离为m,求m的值;
(3)将(1)中的抛物线向上平移t(t>0)个单位,与直线CD交于点G、H,设平移后的抛物线的顶点为D1,与y轴的交点为C1,是否存在实数t,使得DH⊥HD1,若存在,求出t的值;若不存在,说明理由.
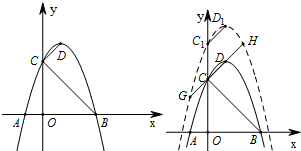
分析:(1)可根据解析式直接得出顶点D的坐标,又可根据CD的长得出C的坐标,代入解析式中即可得出a的值,即得抛物线的解析式;
(2)根据平移的性质写出直线平移后的方程,则第三个点一定是直线MN与抛物线的唯一公共点,联立抛物线的方程,使判别式等于0,即可得出b的平移后的直线方程,作CP⊥MN于P,即可得出m的值;
(3)易判断CC1D1D为平行四边形和△DHD1为等腰直角三角形,由点H在新抛物线上,代入H的坐标,即可得出t的值.
(2)根据平移的性质写出直线平移后的方程,则第三个点一定是直线MN与抛物线的唯一公共点,联立抛物线的方程,使判别式等于0,即可得出b的平移后的直线方程,作CP⊥MN于P,即可得出m的值;
(3)易判断CC1D1D为平行四边形和△DHD1为等腰直角三角形,由点H在新抛物线上,代入H的坐标,即可得出t的值.
解答:解: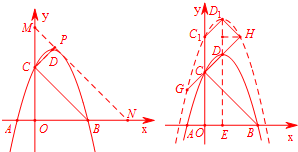 (1)∵D(1,4),CD=
(1)∵D(1,4),CD=
,
∴C(0,3),
∴a=-1,
∴y=-(x-1)2+4,
即y=-x2+2x+3;
(2)∵B(3,0)、C(0,3),
∴直线BC:y=-x+3,将直线BC向上平移b个单位得直线MN:y=-x+3+b,
则第三个点一定是直线MN与抛物线的唯一公共点,
联立
,
消去y得:x2-3x+b=0,
由△=0
得到b=
,
作CP⊥MN于P,则∠CMN=∠OCB=45°,
CM=
,
∴m=CP=
;
(3)由CC1=DD1=t,CC1∥DD1,
∴CC1D1D为平行四边形,
∴C1D1∥CD,
∴∠C1D1D=∠CDE=45°,
∵DH⊥HD1,∴∠DD1H=45°,
即△DHD1为等腰直角三角形,且DD1=t,
∴H(
t+1,
t+4),
由点H在新抛物线y=-x2+2x+3+t上,
∴-(
t+1)2+2(
t+1)+3+t=
t+4,
解得t=2或t=0(舍),
∴t=2.
 (1)∵D(1,4),CD=
(1)∵D(1,4),CD=| 2 |
∴C(0,3),
∴a=-1,
∴y=-(x-1)2+4,
即y=-x2+2x+3;
(2)∵B(3,0)、C(0,3),
∴直线BC:y=-x+3,将直线BC向上平移b个单位得直线MN:y=-x+3+b,
则第三个点一定是直线MN与抛物线的唯一公共点,
联立
|
消去y得:x2-3x+b=0,
由△=0
得到b=
| 9 |
| 4 |
作CP⊥MN于P,则∠CMN=∠OCB=45°,
CM=
| 9 |
| 4 |
∴m=CP=
9
| ||
| 8 |
(3)由CC1=DD1=t,CC1∥DD1,
∴CC1D1D为平行四边形,
∴C1D1∥CD,
∴∠C1D1D=∠CDE=45°,
∵DH⊥HD1,∴∠DD1H=45°,
即△DHD1为等腰直角三角形,且DD1=t,
∴H(
| 1 |
| 2 |
| 1 |
| 2 |
由点H在新抛物线y=-x2+2x+3+t上,
∴-(
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解得t=2或t=0(舍),
∴t=2.
点评:此题考查了抛物线解析式的确定、平行四边形的判定及性质、三角形面积的求法等重要知识点本题的难点在于考虑问题要全面,读懂题意.

练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案
相关题目
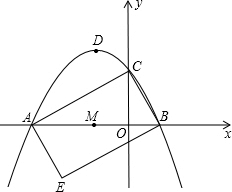 如图抛物线y=
如图抛物线y=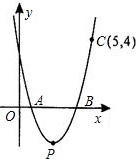 如图抛物线y=ax2-5ax+4a与x轴相交于点A、B,且过点C(5,4).
如图抛物线y=ax2-5ax+4a与x轴相交于点A、B,且过点C(5,4).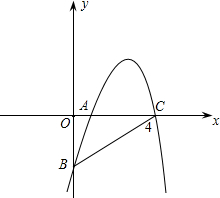 如图抛物线y=-x2+5x+k经过点C(4,0)与x轴交于另一点A,与y轴交于点B.
如图抛物线y=-x2+5x+k经过点C(4,0)与x轴交于另一点A,与y轴交于点B. 如图抛物线y=ax2-5x+4a与x轴相交于点A、B,且过点C(5,4).
如图抛物线y=ax2-5x+4a与x轴相交于点A、B,且过点C(5,4).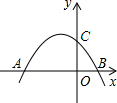 (1996•山东)如图抛物线y=ax2+bx+c,若OB=OC=
(1996•山东)如图抛物线y=ax2+bx+c,若OB=OC=