题目内容
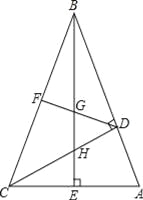
【题目】已知:如图,在△ABC中,AB=BC=10,以AB为直径作⊙O分别交AC,BC于点D,E,连接DE和DB,过点E作EF⊥AB,垂足为F,交BD于点P.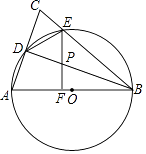
(1)求证:AD=DE;
(2)若CE=2,求线段CD的长;
(3)在(2)的条件下,求△DPE的面积.
【答案】
(1)证明:∵AB是⊙O的直径,
∴∠ADB=90°,
∵AB=BC,
∴D是AC的中点,∠ABD=∠CBD,
∴AD=DE;
(2)解:∵四边形ABED内接于⊙O,
∴∠CED=∠CAB,
∵∠C=∠C,
∴△CED∽△CAB,
∴ ![]() =
= ![]() ,
,
∵AB=BC=10,CE=2,D是AC的中点,
∴CD= ![]() ;
;
(3)解:延长EF交⊙O于M,
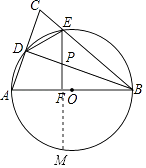
在Rt△ABD中,AD= ![]() ,AB=10,
,AB=10,
∴BD=3 ![]() ,
,
∵EM⊥AB,AB是⊙O的直径,
∴ ![]() =
= ![]() ,
,
∴∠BEP=∠EDB,
∴△BPE∽△BED,
∴ ![]() =
= ![]() ,
,
∴BP= ![]() ,
,
∴DP=BD﹣BP= ![]() ,
,
∴S△DPE:S△BPE=DP:BP=13:32,
∵S△BCD= ![]() ×
× ![]() ×3
×3 ![]() =15,S△BDE:S△BCD=BE:BC=4:5,
=15,S△BDE:S△BCD=BE:BC=4:5,
∴S△BDE=12,
∴S△DPE= ![]() .
.
【解析】(1)AD与DE都是弦,因此可证这两条弦所对的劣弧相等,进而可证弧所对的弦相等,由已知很容易根据等腰三角形性质和直径的性质得证;(2)求线段可采用相似法△CED∽△CAB,根据对应边成比例求出CD;(3)由已知底边、高都不易求,可转化为面积比法,即找一个面积易求的三角形,再求二者的比,通常找△DPE的等高三角形,底边在同一条直线上,它们的面积比等于底边长的比.

练习册系列答案
相关题目