题目内容
【题目】求证:相似三角形对应边上的中线之比等于相似比.
要求:①根据给出的△ABC及线段A'B′,∠A′(∠A′=∠A),以线段A′B′为一边,在给出的图形上用尺规作出△A'B′C′,使得△A'B′C′∽△ABC,不写作法,保留作图痕迹;
②在已有的图形上画出一组对应中线,并据此写出已知、求证和证明过程.

【答案】(1)作图见解析;(2)证明见解析.
【解析】
(1)作∠A'B'C=∠ABC,即可得到△A'B′C′;
(2)依据D是AB的中点,D'是A'B'的中点,即可得到![]() ,根据△ABC∽△A'B'C',即可得到
,根据△ABC∽△A'B'C',即可得到![]() ,∠A'=∠A,进而得出△A'C'D'∽△ACD,可得
,∠A'=∠A,进而得出△A'C'D'∽△ACD,可得![]() .
.
(1)如图所示,△A'B′C′即为所求;
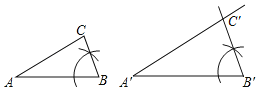
(2)已知,如图,△ABC∽△A'B'C',![]() =k,D是AB的中点,D'是A'B'的中点,
=k,D是AB的中点,D'是A'B'的中点,
求证:![]() =k.
=k.
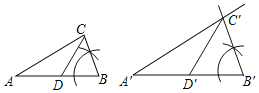
证明:∵D是AB的中点,D'是A'B'的中点,
∴AD=![]() AB,A'D'=
AB,A'D'=![]() A'B',
A'B',
∴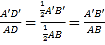 ,
,
∵△ABC∽△A'B'C',
∴![]() ,∠A'=∠A,
,∠A'=∠A,
∵![]() ,∠A'=∠A,
,∠A'=∠A,
∴△A'C'D'∽△ACD,
∴![]() =k.
=k.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目