题目内容
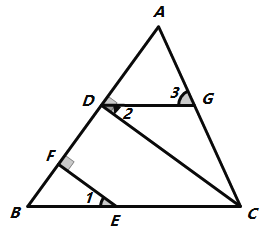
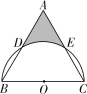
【题目】如图,等边△ABC的边长为4,以BC为直径的半圆O交AB于点D,交AC于点E,则图中阴影部分的面积是( )
A.2![]() -
-![]() B.2
B.2![]() -
-![]()
C.4![]() +-
+-![]() D.4
D.4![]() -
-![]()
【答案】B
【解析】
连接OD、DE、OE,根据菱形的面积公式、扇形面积公式计算,得到答案.
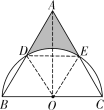
解:如图,连接OD、DE、OE,
∵△ABC为等边三角形,
∴∠B=∠C=60°,
∴∠BOD=60°,∠COE=60°,
∴∠DOE=60°,即△DOE为等边三角形,
∵∠A=∠ODB=60°,
∴OD∥AE,
同理,OE∥AD,
∴四边形ADOE为菱形,
∵△ODE为等边三角形,
∴DE=OD=2,连接AO,
∵四边形ADOE为菱形,
易得OA=![]() ,
,
S菱形ADOE=![]() OA,
OA,
DE=![]() ,
,
∴S阴影=S菱形ADOE-S扇形ODE=![]() -
-![]() =
=![]() -
-![]() .
.
故选B.

【题目】某水果公司以22元/千克的成本价购进1000kg苹果,公司想知道苹果的损坏率,随机抽取若干进行统计,部分结果如下表:
草果总质量n(kg) | 100 | 200 | 300 | 400 | 500 | 1000 |
损坏苹果质量m(kg) | 10.60 | 19.42 | 30.63 | 39.24 | 49.54 | 101.10 |
苹果损坏的频率 (结果保留小数点后三位) | 0.106 | 0.097 | 0.102 | 0.098 | 0.099 | 0.101 |
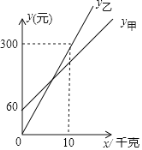
根据此表估计这批苹果损坏的概率(精确到0.1),从而计算该公司希望这批苹果能获得利润23000元,则销售时(去掉损坏的苹果)售价应至少定为_____元/千克.
【题目】某初中学校餐厅为了解学生对早餐的要求,随即抽样调查了该校的部分学生,并根据其中两个单选问题的调查结果,绘制了如下尚不完整的统计图表.
学生能接受的早餐价格统计表
价格分组(单位:元) | 频数 | 频率 |
0<x≤2 | 60 | 0.15 |
2<x≤4 | 180 | c |
4<x≤6 | 92 | 0.23 |
6<x≤8 | a | 0.12 |
x>8 | 20 | 0.05 |
合计 | b | 1 |
根据以上信息解答下列问题:
(1)统计表中,a= ,b= ,c= .
(2)扇形统计图中,m的值为 ,“甜”所对应的圆心角的度数是 .
(3)该餐厅计划每天提供早餐2000份,其中咸味大约准备多少份较好?