题目内容
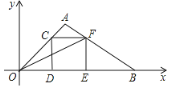
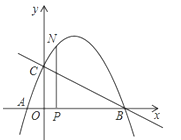
【题目】如图,抛物线与x轴交于点A(﹣![]() , 0),点B(2,0),与y轴交于点C(0,1),连接BC.
, 0),点B(2,0),与y轴交于点C(0,1),连接BC.
(1)求抛物线的解析式;
(2)N为抛物线上的一个动点,过点N作NP⊥x轴于点P,设点N的横坐标为t(﹣![]() <t<2),求△ABN的面积s与t的函数解析式;
<t<2),求△ABN的面积s与t的函数解析式;
(3)若0<t<2且t≠0时,△OPN∽△COB,求点N的坐标.
【答案】(1)y=﹣![]() x2+
x2+![]() x+1;(2)S=﹣
x+1;(2)S=﹣![]() t2+
t2+![]() t+
t+![]() ;(3)点N的坐标为(1,2)
;(3)点N的坐标为(1,2)
【解析】
(1)设抛物线的解析式为y=ax2+bx+c,然后利用待定系数法即可得;
(2)当﹣![]() <t<2时,点N在x轴上方,则NP等于点N的纵坐标,求出AB的长,然后利用三角形面积公式即可得;
<t<2时,点N在x轴上方,则NP等于点N的纵坐标,求出AB的长,然后利用三角形面积公式即可得;
(3)根据相似三角形的性质可得PN=2PO,由于PN=﹣![]() t2+
t2+![]() t+1,PO=|t|=t,可得关于t的方程,解这个方程即可解决这个问题.
t+1,PO=|t|=t,可得关于t的方程,解这个方程即可解决这个问题.
(1)设抛物线的解析式为y=ax2+bx+c,由题意可得: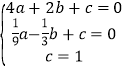 ,
,
解得: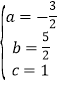 ,
,
∴抛物线的函数关系式为y=﹣![]() x2+
x2+![]() x+1;
x+1;
(2)当﹣![]() <t<2时,yN>0,
<t<2时,yN>0,
∴NP=|yN|=yN=﹣![]() t2+
t2+![]() t+1,
t+1,
∴S=![]() ABPN
ABPN
=![]() ×(2+
×(2+![]() )×(﹣
)×(﹣![]() t2+
t2+![]() t+1)
t+1)
=![]() (﹣
(﹣![]() t2+
t2+![]() t+1)
t+1)
=﹣![]() t2+
t2+![]() t+
t+![]() ;
;
(3)∵△OPN∽△COB,
∴![]() ,
,
∴![]() ,
,
∴PN=2PO,
当0<t<2时,PN=|yN|=yN=﹣![]() t2+
t2+![]() t+1,PO=|t|=t,
t+1,PO=|t|=t,
∴﹣![]() t2+
t2+![]() t+1=2t,
t+1=2t,
整理得:3t2﹣t﹣2=0,
解得:t1=﹣![]() ,t2=1.
,t2=1.
∵﹣![]() <0,0<1<2,
<0,0<1<2,
∴t=1,此时点N的坐标为(1,2),
故点N的坐标为(1,2).

【题目】在学校组织的“最美数学小报”的评比中,校团委给每个同学的作品打分,成绩分为![]() 四个等级,其中相应等级的得分依次记为100分,90分,80分,70分,将八(1)班与八(2)班的成绩整理并绘制成如下统计图:
四个等级,其中相应等级的得分依次记为100分,90分,80分,70分,将八(1)班与八(2)班的成绩整理并绘制成如下统计图:
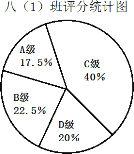

请你根据以上提供的信息解答下列问题:
(1)将表格补充完整.
平均数(分) | 中位数(分) | 众数(分) | |
八(1)班 | 83.75 | 80 | |
八(2)班 | 80 |
(2)若八(1)班有40人,且评分为B级及以上的同学有纪念奖章,请问该班共有几位同学得到奖章?