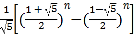题目内容
【题目】如图,在矩形ABCD中,对角线AC、BD相交于点O,点E、F分别是AO、AD的中点,若AB=6cm,BC=8cm,则△AEF的周长=cm.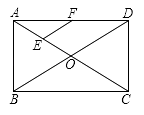
【答案】9
【解析】∵四边形ABCD为矩形,
∴AD=BC,AC=BD,
又∵AB=6cm,BC=8cm
∴AC=BD=10cm,
∴AO=DO=5cm,
又∵点E、F分别是AO、AD的中点,
∴AE=![]() AO=
AO=![]() ,AF=
,AF=![]() AD=4,EF=
AD=4,EF=![]() OD=
OD=![]() ,
,
∴C△AEF=AE+AF+FE=5+4=9.
所以答案是:9.
【考点精析】解答此题的关键在于理解勾股定理的概念的相关知识,掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2,以及对三角形中位线定理的理解,了解连接三角形两边中点的线段叫做三角形的中位线;三角形中位线定理:三角形的中位线平行于三角形的第三边,且等于第三边的一半.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目