题目内容
【题目】如图,△OAB和△OCD中,OA=OB,OC=OD,∠AOB=∠COD=α,AC、BD交于M
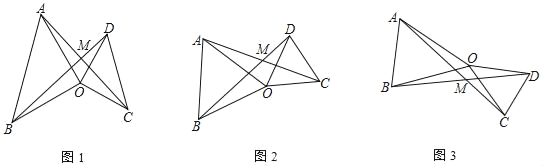
(1)如图1,当α=90°时,∠AMD的度数为 °
(2)如图2,当α=60°时,∠AMD的度数为 °
(3)如图3,当△OCD绕O点任意旋转时,∠AMD与α是否存在着确定的数量关系?如果存在,请你用表示∠AMD,并图3进行证明;若不确定,说明理由.
【答案】(1)90;(2)60;(3)∠AMD=180°﹣α,证明详见解析.
【解析】
(1)如图1中,设OA交BD于K.只要证明△BOD≌△AOC,推出∠OBD=∠OAC,由∠AKM=∠BKO,可得∠AMK=∠BOK=90°;
(2)如图2中,设OA交BD于K.只要证明△BOD≌△AOC,推出∠OBD=∠OAC,由∠AKM=∠BKO,推出∠AMK=∠BOK=60°;
(3)如图3中,设OA交BD于K.只要证明△BOD≌△AOC,可得∠OBD=∠OAC,由∠AKO=∠BKM,推出∠AOK=∠BMK=α.可得∠AMD=180°-α.
(1)如图1中,设OA交BD于K.
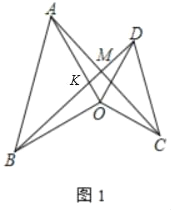
∵OA=OB,OC=OD,∠AOB=∠COD=α,
∴∠BOD=∠AOC,
∴△BOD≌△AOC,
∴∠OBD=∠OAC,
∵∠AKM=∠BKO,
∴∠AMK=∠BOK=90°.
故答案为90.
(2)如图2中,设OA交BD于K.
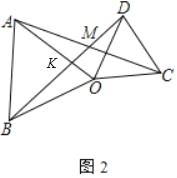
∵OA=OB,OC=OD,∠AOB=∠COD=α,
∴∠BOD=∠AOC,
∴△BOD≌△AOC,
∴∠OBD=∠OAC,
∵∠AKM=∠BKO,
∴∠AMK=∠BOK=60°.
故答案为60.
(3)如图3中,设OA交BD于K.
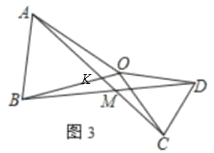
∵OA=OB,OC=OD,∠AOB=∠COD=α,
∴∠BOD=∠AOC,
∴△BOD≌△AOC,
∴∠OBD=∠OAC,
∵∠AKO=∠BKM,
∴∠AOK=∠BMK=α.
∴∠AMD=180°﹣α.

 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案