题目内容
【题目】(本小题7分)如图,一次函数![]() 的图象与x轴交于点B,与反比例函数
的图象与x轴交于点B,与反比例函数![]() 的图象的一个交点为A(2,m).
的图象的一个交点为A(2,m).

(1)求反比例函数的表达式;
(2)求当x满足什么范围时,![]() <
<![]() ;
;
(3)过点A作AC⊥x轴,垂足为点C,如果求点P在反比例函数图象上,且△PBC的面积等于6,请直接写出点P的坐标.
【答案】(1)![]() ; (2)
; (2)![]() ; (3) (3,2)(-3,-2)
; (3) (3,2)(-3,-2)
【解析】
试题(1)先将点A(2,m)代入反比例函数![]() 求得A的坐标,然后代入
求得A的坐标,然后代入![]() ,求得k的值(2)首先求出两函数交点的坐标,再结合反比例函数和一次函数的图像即可求出:
,求得k的值(2)首先求出两函数交点的坐标,再结合反比例函数和一次函数的图像即可求出:![]() 的解集.
的解集.
(3) 可求得点B的坐标,设P(x,y),由![]() ,即可求得x,y的值.
,即可求得x,y的值.
试题解析:
解;(1)∵一次函数![]() 的图象经过点A,
的图象经过点A,
∴m=3,
∴点A的坐标为(2,3),
∵反比例函数![]() 的图象经过点A(2,3),
的图象经过点A(2,3),
∴k=6,
∴反比例函数的表达式:![]() .
.
(2)联立反比例函数和一次函数的解析式:
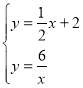
解得:![]() 或
或![]() ,
,
∴![]() 的解集为x<-6或0﹤x﹤2;
的解集为x<-6或0﹤x﹤2;
(3)令![]() ,解得:x=-4,即B(-4,0),
,解得:x=-4,即B(-4,0),
∵AC⊥x轴
∴C(2,0),
∴BC=6,
设P(x,y),
∵![]()
∴![]() 或
或![]() ,
,
分别代入![]() 中,
中,
得![]() 或
或![]()
∴P(3,2)或P(-3,-2).

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目