题目内容
1.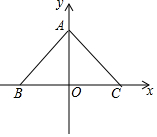 如图,在平面直角坐标系中,点O为坐标原点,△ABC的顶点A在y轴的正半轴上,且OA=m,顶点B,C的坐标分别为(-m,0),(m,0),点D是线段AB上的一个动点(点D不与点A、B重合),点E是线段AC上的一点,且AE=BD,连接OD,DE,线段DE与线段OA相交于点F;
如图,在平面直角坐标系中,点O为坐标原点,△ABC的顶点A在y轴的正半轴上,且OA=m,顶点B,C的坐标分别为(-m,0),(m,0),点D是线段AB上的一个动点(点D不与点A、B重合),点E是线段AC上的一点,且AE=BD,连接OD,DE,线段DE与线段OA相交于点F;(1)求∠ODE的度数;
(2)当m=2+2$\sqrt{2}$,且△ODF为等腰三角形时,求点D的坐标;
(3)连接CD,过点C作CG⊥DE交线段DE的延长线于点G,过点F作FH∥AB交线段CG的延长线于点H,若∠ADE=∠CDE,求证:CH-2EG=$\frac{BD•DF}{AD}$.
分析 (1)只要证明△OBD≌△OAE,OD=OE,∠BOD=∠AOE,∠DOE=∠BOA=90°,推出△DOE是等腰直角三角形即可.
(2)分两种情形讨论即可解决问题①当点D是AB中点时,△DOF是等腰三角形,此时D(-1-$\sqrt{2}$,1+$\sqrt{2}$).②当DF=DO时,∠DOF=∠DFO=∠ADO,推出AD=AO,求出BD即可解决问题.
(3)如图3中,延长BA交CH的延长线于N,连接CF、OG.只要证明△FHG≌△CEG,推出EG=HG,由FA平分∠DAE,推出$\frac{AD}{AE}$=$\frac{DF}{EF}$,(角平分线性质定理),推出DF•AE=AD•EF,由BD=AE,推出DF•BD=AD•EF,推出$\frac{BD•DF}{AD}$=EF,CH-2EG=(GH+CG)-2EG=EF,延长即可证明.
解答 解:(1)如图1中,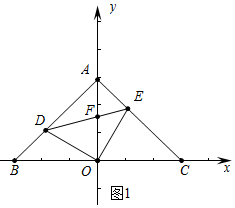
∵OA=OB=OC,OA⊥BC,
∴△ABC是等腰直角三角形,
∴∠OBD=∠OAE=45°,
在△OBD和△OAE中,
$\left\{\begin{array}{l}{OB=OA}\\{∠OBD=∠OAE}\\{BD=AE}\end{array}\right.$,
∴△OBD≌△OAE,
∴OD=OE,∠BOD=∠AOE,
∴∠DOE=∠BOA=90°,
∴∠ODE=45°.
(2)如图2中,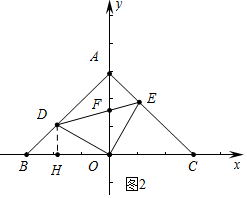
①当点D是AB中点时,△DOF是等腰三角形,此时D(-1-$\sqrt{2}$,1+$\sqrt{2}$).
②当DF=DO时,∠DOF=∠DFO=∠ADO,
∴AD=AO,
∴BD=2$\sqrt{2}$+4-(2+2$\sqrt{2}$)=2,
∵∠DBH=∠BDH=45°,
∴DB=DH=$\sqrt{2}$,
∴D(-2-$\sqrt{2}$,$\sqrt{2}$),
综上所述,满足条件的点D坐标(-1-$\sqrt{2}$,1+$\sqrt{2}$)或(-2-$\sqrt{2}$,$\sqrt{2}$).
(3)如图3中,延长BA交CH的延长线于N,连接CF、OG.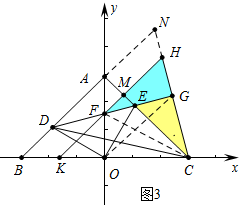
∵∠GDN=∠GDC,DG⊥CN,
∴∠N=∠DCG,
∴DN=DC,GN=GC,
∵CO=OB,
∴OG∥BN,∵KH∥BN,
∴OG∥BN,
∴∠GOC=45°,
∵∠FOC+∠FGC=180°,
∴F、O、C、G四点共圆,
∴∠GFC=∠GOC=45°,
∴∠GFC=∠GCF=45°,
∴FG=GC,
在△FHG和△CEG中,
$\left\{\begin{array}{l}{∠FGH=∠CGF}\\{∠HFG=∠ECG}\\{FG=GC}\end{array}\right.$,
∴△FHG≌△CEG,
∴EG=HG,
∵FA平分∠DAE,
∴$\frac{AD}{AE}$=$\frac{DF}{EF}$,(角平分线性质定理)
∴DF•AE=AD•EF,
∵BD=AE,
∴DF•BD=AD•EF,
∴$\frac{BD•DF}{AD}$=EF,CH-2EG=(GH+CG)-2EG=EF,
∴CH-2EG=$\frac{BD•DF}{AD}$.
点评 本题考查三角形综合题、全等三角形的判定和性质、角平分线的性质定理、四点共圆等知识,解题的关键是学会利用四点共圆,角平分线的性质定理解决问题,题目比较难,知识点比较多,属于中考压轴题.

 53随堂测系列答案
53随堂测系列答案| A. | 正数的相反数是它本身 | B. | 任何有理数的绝对值都大于0 | ||
| C. | 0的倒数是0 | D. | 最大的负整数是-1 |
| A. | x>0 | B. | x为一切实数 | C. | y>2 | D. | y为一切实数 |
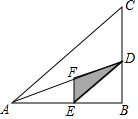 如图,己知AD、DE、EF分别是△ABC、△ABD、△AED的中线,若S△ABC=24cm2,则阴影部分△DEF的面积为3cm2.
如图,己知AD、DE、EF分别是△ABC、△ABD、△AED的中线,若S△ABC=24cm2,则阴影部分△DEF的面积为3cm2. 如图,⊙O的直径AB为10cm,弦BC为5cm,D、E分别是∠ACB的平分线与⊙O,AB的交点,P为AB延长线上一点,且PC=PE.
如图,⊙O的直径AB为10cm,弦BC为5cm,D、E分别是∠ACB的平分线与⊙O,AB的交点,P为AB延长线上一点,且PC=PE.