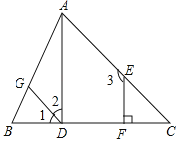
题目内容
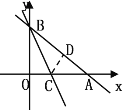
【题目】如图,直线y=﹣2x+7与x轴、y轴分别相交于点C、B,与直线y=![]() x相交于点A.
x相交于点A.
(1)求A点坐标;
(2)求△OAC的面积;
(3)如果在y轴上存在一点P,使△OAP是以OA为底边的等腰三角形,求P点坐标;
(4)在直线y=﹣2x+7上是否存在点Q,使△OAQ的面积等于6?若存在,请求出Q点的坐标,若不存在,请说明理由.

【答案】(1)A点坐标是(2,3);(2)![]() =
=![]() ;(3)P点坐标是(0,
;(3)P点坐标是(0, ![]() );(4)点Q是坐标是(
);(4)点Q是坐标是(![]() ,
,![]() )或(
)或(![]() ,-
,-![]() ).
).
【解析】
解析
联立方程,解方程即可求得;
C点位直线y=﹣2x+7与x轴交点,可得C点坐标为(![]() ,0),由(1)得A点坐标,可得
,0),由(1)得A点坐标,可得![]() 的值;
的值;
(3)设P点坐标是(0,y),根据勾股定理列出方程,解方程即可求得;
(4)分两种情况:①当Q点在线段AB上:作QD⊥y轴于点D,则QD=x,根据
![]() =
=![]() -
-![]() 列出关于x的方程解方程求得即可;②当Q点在AC的延长线上时,作QD⊥x轴于点D,则QD=-y,根据
列出关于x的方程解方程求得即可;②当Q点在AC的延长线上时,作QD⊥x轴于点D,则QD=-y,根据![]() =
=![]() -
- ![]() 列出关于y的方程解方程求得即可.
列出关于y的方程解方程求得即可.
解(1)解方程组: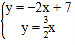 得:
得:![]() ,
,
![]() A点坐标是(2,3);
A点坐标是(2,3);
(2)![]() C点位直线y=﹣2x+7与x轴交点,可得C点坐标为(
C点位直线y=﹣2x+7与x轴交点,可得C点坐标为(![]() ,0)
,0)
![]()
![]() =
=![]() =
=![]()
(3)设P点坐标是(0,y ),
![]() △OAP是以OA为底边的等腰三角形,
△OAP是以OA为底边的等腰三角形,
![]() OP=PA,
OP=PA,
![]()
![]() ,
,
解得y=![]() ,
,
![]() P点坐标是(0,
P点坐标是(0, ![]() ),
),
故答案为(0, ![]() );
);
(4)存在;
由直线y=-2x+7可知B(0,7),C(![]() ,0),
,0),
![]()
![]() =
=![]() =
=![]() <6,
<6,
![]() =
=![]() =7>6,
=7>6,
![]() Q点有两个位置:Q在线段AB上和AC的延长线上,设点Q的坐标是(x,y),
Q点有两个位置:Q在线段AB上和AC的延长线上,设点Q的坐标是(x,y),
当Q点在线段AB上:作QD⊥y轴于点D,如图1, 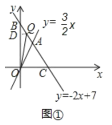
则QD=x,![]()
![]() =
=![]() -
-![]() =7-6=1,
=7-6=1,
![]()
![]() OB
OB![]() QD=1,即:
QD=1,即: ![]()
![]() 7x=1,
7x=1,
![]() x=
x=![]() ,
,
把x=![]() 代入y=-2x+7,得y=
代入y=-2x+7,得y=![]() ,
,
![]() Q的坐标是(
Q的坐标是(![]() ,
,![]() ),
),
当Q点在AC的延长线上时,作QD⊥x轴于点D,如图2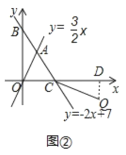
则QD=-y,
![]()
![]() =
=![]() -
- ![]() =6-
=6-![]() =
=![]() ,
,
![]()
![]() OC
OC![]() QD=
QD=![]() ,即:
,即:![]() ,
,
![]() y=-
y=-![]() ,
,
把y=-![]() 代入y=-2x+7,解得x=
代入y=-2x+7,解得x=![]()
![]() Q的坐标是(
Q的坐标是(![]() ,-
,-![]() ),
),
综上所述:点Q是坐标是(![]() ,
,![]() )或(
)或(![]() ,-
,-![]() ).
).

 口算能手系列答案
口算能手系列答案