题目内容
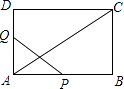
【题目】如图,在平面直角坐标系中,矩形ABCO的边OC、OA,分别在x轴、y轴上,点E在边BC上,将该矩形沿AE折叠,点B恰好落在边OC上的F处,若OA=8,CF=4,则点E的坐标是 . 
【答案】(-10,3)
【解析】解:∵矩形ABCO中,
∴CE∥AO.
∴△CEF∽△OFA.
∴![]() =
=![]() .
.
又∵OA=8,CF=4.
∴OF=2CE.
设CE=x,则BE=8-x.
根据折叠的性质,可得EF=8-x.
∴![]() ,
,
∴x=3,
∴OF=6,
∴OC=10,
∴点E的坐标为(-10,3).
故答案为:(-10,3)
根据题意可知△CEF∽△OFA,可根据相似三角形的性质对应边成比例,可求得OF=2CE,设CE=x,则BE=8-x,然后根据折叠的性质,可得EF=8-x,根据勾股定理可得 x 2 + 4 2 = ( 8 x ) 2 ,解得x=3,则OF=6,所以OC=10,由此可得点E的坐标为(-10,3).

练习册系列答案
相关题目